题目内容
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知acosC+ccosA=2bcosA.
(1)求角A的值;
(2)求sinB+sinC的取值范围.
解:(1)因为acosC+ccosA=2bcosA,所以sinAcosC+sinCcosA=2sinBcosA,
即sin(A+C)=2sinBcosA.
因为A+B+C=π,所以sin(A+C)=sinB.
从而sinB=2sinBcosA.
因为sinB≠0,所以cosA=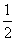 .
.
因为0<A<π,所以A= .
.
(2)sinB+sinC=sinB+sin( -B)=sinB+sin
-B)=sinB+sin cosB-cos
cosB-cos sinB
sinB
=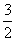 sinB+
sinB+ cosB=
cosB=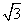 sin(B+
sin(B+ ).
).
因为0<B< ,所以
,所以 .
.
所以sinB+sinC的取值范围为( ,
,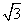 ].
].

练习册系列答案
相关题目
 ,f(x)=
,f(x)=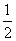 x,求使f(x)=-
x,求使f(x)=-
 .
. 则z=2x+y的最大值是 .
则z=2x+y的最大值是 .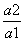 的值;
的值; ,
, ,则
,则 = .
= .  为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点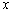 米,圆心角为
米,圆心角为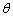 (弧度).
(弧度).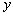 ,求
,求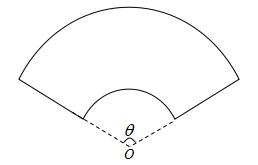
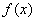 满足
满足 ,且
,且 ,则不等式
,则不等式 .
.