题目内容
圆x2+y2+ax+by=0与直线ax+by=0(a2+b2≠0)的位置关系是
- A.直线与圆相交但不过圆心
- B.相切
- C.直线与圆相交且过圆心
- D.相离
B
分析:将圆的方程化为标准方程,表示出圆心坐标和半径r,利用点到直线的距离公式求出圆心到已知直线的距离d,由d=r可得出直线与圆位置关系是相切.
解答:将圆的方程化为标准方程得:(x+ )2+(y+
)2+(y+ )2=
)2= ,
,
∴圆心坐标为(- ,-
,- ),半径r=
),半径r=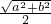 ,
,
∵圆心到直线ax+by=0的距离d= =
=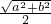 =r,
=r,
则圆与直线的位置关系是相切.
故选B
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,直线与圆相切时,圆心到直线的距离等于圆的半径,熟练掌握此性质是解本题的关键.
分析:将圆的方程化为标准方程,表示出圆心坐标和半径r,利用点到直线的距离公式求出圆心到已知直线的距离d,由d=r可得出直线与圆位置关系是相切.
解答:将圆的方程化为标准方程得:(x+
 )2+(y+
)2+(y+ )2=
)2= ,
,∴圆心坐标为(-
 ,-
,- ),半径r=
),半径r=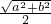 ,
,∵圆心到直线ax+by=0的距离d=
 =
=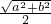 =r,
=r,则圆与直线的位置关系是相切.
故选B
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,直线与圆相切时,圆心到直线的距离等于圆的半径,熟练掌握此性质是解本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目