题目内容
若实数x，y满足x2+y2+xy=1，则x+y的最大值是 ．
【答案】分析：利用基本不等式，根据xy≤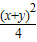
把题设等式整理成关于x+y的不等式，求得其范围，则x+y的最大值可得．
解答：解：∵x2+y2+xy=1
∴（x+y）2=1+xy
∵xy≤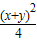
∴（x+y）2-1≤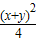
，整理求得-
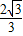≤x+y≤
∴x+y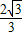的最大值是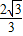
故答案为：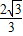
点评：本题主要考查了基本不等式．应熟练掌握如均值不等式，柯西不等式等性质．
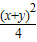把题设等式整理成关于x+y的不等式，求得其范围，则x+y的最大值可得．解答：解：∵x2+y2+xy=1
∴（x+y）2=1+xy
∵xy≤
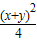
∴（x+y）2-1≤
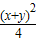，整理求得-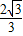≤x+y≤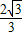∴x+y的最大值是
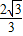
故答案为：
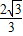
点评：本题主要考查了基本不等式．应熟练掌握如均值不等式，柯西不等式等性质．
练习册系列答案
阅读快车系列答案
相关题目
若实数x，y满足x2+y2-4x+1=0，则
的最小值是（ ）
| y |
| x |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|