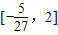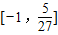题目内容
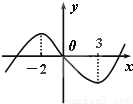
 如图所示是函数f(x)=x3+bx2+3cx+d的大致图象,方程x3+
如图所示是函数f(x)=x3+bx2+3cx+d的大致图象,方程x3+| 2 |
| 3 |
| c |
| 6 |
分析:先利用函数f(x)的图象,知函数过原点,且有两个极值点,即f(0)=0,f′(-2)=0,f′(3)=0,代入解析式即可解得b、c、d的值,再将方程x3+
bx2+
x-m=0在x∈[-2,2]内有解问题转化为求函数g(x)=x3-x2-x,的值域问题,利用导数求其在闭区间[-2,2]内的最值即可
| 2 |
| 3 |
| c |
| 6 |
解答:解:由函数f(x)的图象可知:f(0)=0,f′(-2)=0,f′(3)=0
∵f(x)=x3+bx2+3cx+d,f′(x)=3x2+2bx+3c
∴
解得:b=-
,c=-6,d=0
∴方程x3+
bx2+
x-m=0在x∈[-2,2]内有解,即方程x3-x2-x-m=0在x∈[-2,2]内有解,
即m=x3-x2-x在x∈[-2,2]内有解,
设g(x)=x3-x2-x,则g′(x)=3x2-2x-1=(x-1)(3x+1)
∴当x∈[-2,-
]时,g′(x)>0,g(x)为增函数,当x∈[-
,1]时,g′(x)<0,g(x)为减函数,当x∈[1,2]时,g′(x)>0,g(x)为增函数,
而g(-2)=-10,g(-
)=
,g(1)=-1,g(2)=2
∴g(x)∈[-10,2]
即m∈[-10,2]
故选 B
∵f(x)=x3+bx2+3cx+d,f′(x)=3x2+2bx+3c
∴
|
| 3 |
| 2 |
∴方程x3+
| 2 |
| 3 |
| c |
| 6 |
即m=x3-x2-x在x∈[-2,2]内有解,
设g(x)=x3-x2-x,则g′(x)=3x2-2x-1=(x-1)(3x+1)
∴当x∈[-2,-
| 1 |
| 3 |
| 1 |
| 3 |
而g(-2)=-10,g(-
| 1 |
| 3 |
| 5 |
| 27 |
∴g(x)∈[-10,2]
即m∈[-10,2]
故选 B
点评:本题主要考查了导数与函数极值点之间的关系,利用导数求函数在闭区间上的最值的方法,将方程有解问题转化为函数值域问题中转化化归的思想方法

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
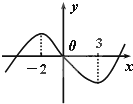
 如图所示,函数f(x)的图象在P点处的切线方程是y=-x+8,则f′(5)=
如图所示,函数f(x)的图象在P点处的切线方程是y=-x+8,则f′(5)=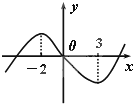 如图所示是函数f(x)=x3+bx2+3cx+d的大致图象,方程
如图所示是函数f(x)=x3+bx2+3cx+d的大致图象,方程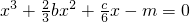 在x∈[-2,2]内有解,则m的取值范围是
在x∈[-2,2]内有解,则m的取值范围是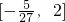
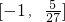
 在x∈[-2,2]内有解,则m的取值范围是( )
在x∈[-2,2]内有解,则m的取值范围是( )