题目内容
设函数 ,且
,且 ,其中p≥0,e是自然对数的底数.
,其中p≥0,e是自然对数的底数.(1)求p与q的关系;
(2)若f(x)在其定义域内为单调函数,求p的取值范围.
(3)设
 .若存在x∈[1,e],使得f(x)>g(x)成立,求实数p的取值范围.
.若存在x∈[1,e],使得f(x)>g(x)成立,求实数p的取值范围.
【答案】分析:(1)根据函数 ,且
,且 ,可得(p-q)(
,可得(p-q)( )=0,从而可求p与q的关系;
)=0,从而可求p与q的关系;
(2)求导函数,再进行分类讨论:当p=0时,f(x)在其定义域(0,+∞)内为单调减函数;当p>0时,要使f(x)在其定义域(0,+∞)内为单调函数,只需h(x)在(0,+∞)内满足h(x)≥0恒成立,从而可求p的取值范围;(3)确定 在[1,e]上的最值,再分类讨论:①当p=0时,f(x)min=f(1)=0,不合题意;②当p≥1时,只需f(x)max>g(x)min(x∈[1,e]);③当0<p<1时,不合题意,从而可求实数p的取值范围是.
在[1,e]上的最值,再分类讨论:①当p=0时,f(x)min=f(1)=0,不合题意;②当p≥1时,只需f(x)max>g(x)min(x∈[1,e]);③当0<p<1时,不合题意,从而可求实数p的取值范围是.
解答:解:(1)由题意,∵函数 ,且
,且 ,∴(p-q)(
,∴(p-q)( )=0
)=0
∵ ≠0,∴p-q=0,∴p=q
≠0,∴p-q=0,∴p=q
(2)由(1)知, ,求导函数,可得f′(x)=
,求导函数,可得f′(x)=
当p=0时,f′(x)=- <0,所以f(x)在其定义域(0,+∞)内为单调减函数
<0,所以f(x)在其定义域(0,+∞)内为单调减函数
当p>0时,要使f(x)在其定义域(0,+∞)内为单调函数,由于h(x)=px2-2x+p图象为开口向上的抛物线,所以只需h(x)在(0,+∞)内满足h(x)≥0恒成立
函数h(x)=px2-2x+p的对称轴为 ,∴
,∴
∴只需 ,∵p>0,∴p≥1
,∵p>0,∴p≥1
综上所述,p的取值范围为{0}∪[1,+∞)
(3)∵ 在[1,e]上是减函数,
在[1,e]上是减函数,
∴x=e时,g(x)min=2;x=1时,g(x)max=2e,即g(x)∈[2,2e]
①当p=0时,由(2)知f(x)在[1,e]上是减函数,∴f(x)min=f(1)=0,不合题意;
②当p≥1时,由(2)知f(x)在[1,e]上是增函数,f(1)=0<2,
又 在[1,e]上是减函数,故只需f(x)max>g(x)min(x∈[1,e]),
在[1,e]上是减函数,故只需f(x)max>g(x)min(x∈[1,e]),
∵f(x)max=f(e)=p(e- )-2,g(x)min=2,
)-2,g(x)min=2,
∴p(e- )-2>2,∴
)-2>2,∴ ;
;
③当0<p<1时,由x∈[1,e], ≥0,
≥0,
由(2)知当p=1时,f(x)在[1,e]上是增函数, ≤
≤ ≤
≤ 2,不合题意
2,不合题意
综上,实数p的取值范围是 .
.
点评:本题考查导数知识的运用,考查函数的单调性,考查存在性问题,考查分类讨论的数学思想,考查学生分析解决问题的能力,综合性强.
 ,且
,且 ,可得(p-q)(
,可得(p-q)( )=0,从而可求p与q的关系;
)=0,从而可求p与q的关系;(2)求导函数,再进行分类讨论:当p=0时,f(x)在其定义域(0,+∞)内为单调减函数;当p>0时,要使f(x)在其定义域(0,+∞)内为单调函数,只需h(x)在(0,+∞)内满足h(x)≥0恒成立,从而可求p的取值范围;(3)确定
 在[1,e]上的最值,再分类讨论:①当p=0时,f(x)min=f(1)=0,不合题意;②当p≥1时,只需f(x)max>g(x)min(x∈[1,e]);③当0<p<1时,不合题意,从而可求实数p的取值范围是.
在[1,e]上的最值,再分类讨论:①当p=0时,f(x)min=f(1)=0,不合题意;②当p≥1时,只需f(x)max>g(x)min(x∈[1,e]);③当0<p<1时,不合题意,从而可求实数p的取值范围是.解答:解:(1)由题意,∵函数
 ,且
,且 ,∴(p-q)(
,∴(p-q)( )=0
)=0∵
 ≠0,∴p-q=0,∴p=q
≠0,∴p-q=0,∴p=q(2)由(1)知,
 ,求导函数,可得f′(x)=
,求导函数,可得f′(x)=
当p=0时,f′(x)=-
 <0,所以f(x)在其定义域(0,+∞)内为单调减函数
<0,所以f(x)在其定义域(0,+∞)内为单调减函数当p>0时,要使f(x)在其定义域(0,+∞)内为单调函数,由于h(x)=px2-2x+p图象为开口向上的抛物线,所以只需h(x)在(0,+∞)内满足h(x)≥0恒成立
函数h(x)=px2-2x+p的对称轴为
 ,∴
,∴
∴只需
 ,∵p>0,∴p≥1
,∵p>0,∴p≥1综上所述,p的取值范围为{0}∪[1,+∞)
(3)∵
 在[1,e]上是减函数,
在[1,e]上是减函数,∴x=e时,g(x)min=2;x=1时,g(x)max=2e,即g(x)∈[2,2e]
①当p=0时,由(2)知f(x)在[1,e]上是减函数,∴f(x)min=f(1)=0,不合题意;
②当p≥1时,由(2)知f(x)在[1,e]上是增函数,f(1)=0<2,
又
 在[1,e]上是减函数,故只需f(x)max>g(x)min(x∈[1,e]),
在[1,e]上是减函数,故只需f(x)max>g(x)min(x∈[1,e]),∵f(x)max=f(e)=p(e-
 )-2,g(x)min=2,
)-2,g(x)min=2,∴p(e-
 )-2>2,∴
)-2>2,∴ ;
;③当0<p<1时,由x∈[1,e],
 ≥0,
≥0,由(2)知当p=1时,f(x)在[1,e]上是增函数,
 ≤
≤ ≤
≤ 2,不合题意
2,不合题意综上,实数p的取值范围是
 .
.点评:本题考查导数知识的运用,考查函数的单调性,考查存在性问题,考查分类讨论的数学思想,考查学生分析解决问题的能力,综合性强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(理)如图,平面ADEF⊥平面ABCD,ABCD与ADEF均为矩形,且AB:AD:AF=
|
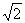 :2:
:2: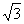 ;P为线段EF上一点,M为AB的中点,若PC与BD所成的角为
;P为线段EF上一点,M为AB的中点,若PC与BD所成的角为
60°.
(1)试确定P点位置;
(2)求二面角P—MC—D的大小的余弦值;
(3)当AB长为多少时,点D到平面PMC的距离等于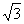 ?
?
(文)设函数 (
( ),其中
),其中 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的极大值和极小值;
的极大值和极小值;
(Ⅲ)当 时,证明存在
时,证明存在 ,使得不等式
,使得不等式 对任意的
对任意的 恒成立.
恒成立.




 ,且
,且 ,其中p≥0,e是自然对数的底数.
,其中p≥0,e是自然对数的底数. .若存在x0∈[1,e],使得f(x0)>g(x0)成立,求实数p的取值范围.
.若存在x0∈[1,e],使得f(x0)>g(x0)成立,求实数p的取值范围.