题目内容
将函数y=sin(2x-
)的图象先向右平移
，然后将得到的图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），则所得到的图象对应函数解析式为（ ）
| π |
| 3 |
| π |
| 12 |
分析：根据三角函数图象变换的公式，结合诱导公式进行化简，可得两次变换后所得到的图象对应函数解析式．
解答：解：设f（x）=sin(2x-
)，可得y=f（x）的图象向右平移
，
得到f（x-
）=sin[2(x-
)-
]=sin(2x-
)的图象，
再将所得的图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），可得f（
x-
）=sin(x-
)=-cosx的图象．
∴函数y=sin(2x-
)的图象按题中的两步变换，最终得到的图象对应函数解析式为y=-cosx，
故选：D
| π |
| 3 |
| π |
| 12 |
得到f（x-
| π |
| 12 |
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
再将所得的图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），可得f（
| 1 |
| 2 |
| π |
| 12 |
| π |
| 2 |
∴函数y=sin(2x-
| π |
| 3 |
故选：D
点评：本题给出三角函数图象的平移和伸缩变换，求得到的图象对应的函数解析式．着重考查了三角函数图象的变换公式和诱导公式等知识，属于基础中档题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
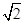cos(2
+
)的图象, 只需要将函数y=
个单位，纵坐标不变；