题目内容
若函数
和
的定义域、值域都是
，则不等式
有解的充要条件是（ ）
A． |
B．有无穷多个 ，使得 |
C． |
D． |
A
解析试题分析：该题主要考察审题能力及数学文字语言与数学符号语言之间的转化问题，依题意，只须保证不等式有解，而不是有无数解，也不是解集为全体实数，B表示有无数个解，C、D表示不等式的解集为，A选项符合要求，故选A.
考点：1.全称量词与存在量词；2.充分必要条件.
练习册系列答案
相关题目
若命题
：
，
：
，则是的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
已知
，
，则
是
成立的 ( )
| A．必要不充分条件 | B．充分不必要条件 |
| C．充要条件 | D．既不充分又不必要条件 |
“－3＜m＜5”是“方程
表示椭圆”的 ( )．
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
设条件
；条件
，那么
是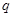
的（ ） 条件
| A．充分非必要 | B．必要非充分 | C．充分且必要 | D．非充分非必要 |
使命题“对任意的x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是( )
| A．a≥4 | B．a≤4 |
| C．a≥5 | D．a≤5 |
设a,b∈R,则“a>1且0<b<1”是“a-b>0且
>1”的( )
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
设a，b∈R，则“(a－b)·a2<0”是“a<b”的 ( )．
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
下列说法错误的是：( )．
| A．命题“若x2－4x＋3＝0，则x＝3”的逆否命题是“若x≠3”，则x2－4x+3≠0” |
| B．“x>1”是“|x|>0”的充分不必要条件 |
| C．若p∧q为假命题，则p，q均为假命题 |
| D．命题p：“?x∈R，使得x2＋x＋1<0”，则綈p：“?x∈R，x2＋x＋1≥0” |