题目内容
(2012•广东模拟)已知f(x)为定义在(-∞,+∞)上的可导函数,且f(x)<f′(x)对于x∈R恒成立,且e为自然对数的底,则( )
分析:构造函数y=
的导数形式,并判断增减性,从而得到答案.
| f(x) |
| ex |
解答:解:∵f(x)<f'(x) 从而 f'(x)-f(x)>0 从而
>0
即[
]′>0,所以函数y=
单调递增,
故当x>0时,
>
=f(0),整理得出f(x)>exf(0)
当x=1时f(1)>e•f(0),
当x=2012时f(2012)>e2012•f(0).
故选A.
| ex[f′(x)-f(x)] |
| e2x |
即[
| f(x) |
| ex |
| f(x) |
| ex |
故当x>0时,
| f(x) |
| ex |
| f(0) |
| e0 |
当x=1时f(1)>e•f(0),
当x=2012时f(2012)>e2012•f(0).
故选A.
点评:本题主要考查函数的单调性与其导函数的关系,函数单调性的关系,考查转化、构造、计算能力.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
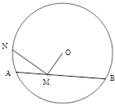 (2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=
(2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=