题目内容
已知函数
(1)当 时,求函数
时,求函数 在
在 上的极值;
上的极值;
(2)证明:当 时,
时, ;
;
(3)证明:
 .
.
(1)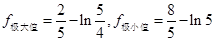 ;(2)证明过程详见解析;(3)证明过程详见解析.
;(2)证明过程详见解析;(3)证明过程详见解析.
解析试题分析:本题主要考查导数的运算,利用导数研究函数的单调性、极值和最值、不等式等基础知识,考查函数思想,考查综合分析和解决问题的能力.第一问,将 代入,得到
代入,得到 解析式,对它求导,列出表格,通过单调性,判断极值;第二问,证明不等式转化为求函数
解析式,对它求导,列出表格,通过单调性,判断极值;第二问,证明不等式转化为求函数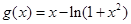 的最小值大于0;第三问,利用第二问的结论,令
的最小值大于0;第三问,利用第二问的结论,令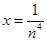 ,利用放缩法得到
,利用放缩法得到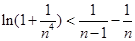 ,再利用对数的性质和裂项相消法求和,得到所证不等式.
,再利用对数的性质和裂项相消法求和,得到所证不等式.
试题解析:(1)当 时,
时,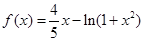
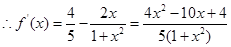 1分
1分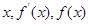 变化如下表
变化如下表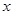
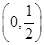
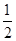
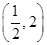

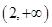
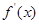
+ 0 0 + 
↗ 极大值 
↘ 极小值 ↗ 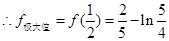 ,
, 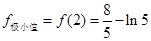 4分
4分
(2)令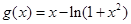
则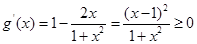 6分
6分
∴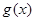 在
在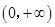 上为增函数。
上为增函数。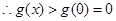 8分
8分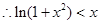 9分
9分
(3)由(2)知
 10分
10分
令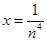 得,
得,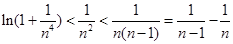 12分
12分
练习册系列答案
相关题目
 .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; 的单调性.
的单调性.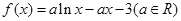 。
。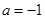 ,求函数
,求函数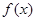 的单调区间并比较
的单调区间并比较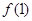 的大小关系
的大小关系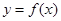 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为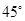 ,对于任意的
,对于任意的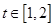 ,函数
,函数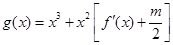 在区间
在区间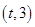 上总不是单调函数,求
上总不是单调函数,求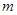 的取值范围;
的取值范围;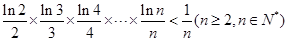 。
。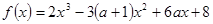 ,其中
,其中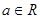 .
.  在
在 处取得极值,求常数
处取得极值,求常数 的值;
的值; ,
, ,若
,若 元素中有唯一的整数,求
元素中有唯一的整数,求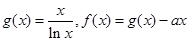 .
.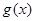 的单调区间;
的单调区间; 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值;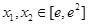 (
(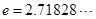 是自然对数的底数)使
是自然对数的底数)使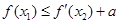 ,求实数
,求实数 ,
, 的极值点;
的极值点; 过点
过点 ,并且与曲线
,并且与曲线 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数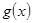 在
在 上的最小值(其中
上的最小值(其中 为自然对数的底数).
为自然对数的底数).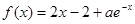 (
(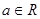 )
) 在点
在点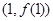 处的切线平行于
处的切线平行于 轴,求
轴,求 的值;
的值;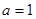 时,若直线
时,若直线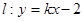 与曲线
与曲线 上有公共点,求
上有公共点,求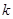 的取值范围.
的取值范围.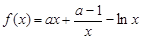
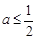 时,试讨论函数
时,试讨论函数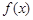 的单调性;
的单调性;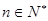 ,有
,有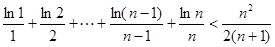 .
.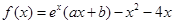 ,曲线
,曲线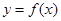 在点
在点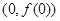 处切线方程为
处切线方程为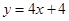 。
。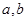 的值;
的值;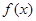 的单调性,并求
的单调性,并求