题目内容
已知数列{an}满足a1=2,10a n+1﹣9an﹣1=0, .
.
(1)求证:数列{an﹣1}是等比数列;
(2)当n取何值时,bn取最大值;
(3)若 对任意m∈N*恒成立,求实数t的取值范围.
对任意m∈N*恒成立,求实数t的取值范围.
 .
.(1)求证:数列{an﹣1}是等比数列;
(2)当n取何值时,bn取最大值;
(3)若
 对任意m∈N*恒成立,求实数t的取值范围.
对任意m∈N*恒成立,求实数t的取值范围. (1)证明:∵a10an+1﹣9an﹣1=0,
∴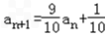 .
.
∴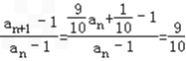 ,
,
∵a1=2,
∴{an﹣1}是以a1﹣1=1为首项,公比为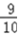 的等比数列.
的等比数列.
(2)解:由( 1),可知an﹣1=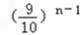 (n∈N*). ∴
(n∈N*). ∴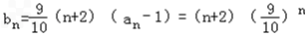 ,
,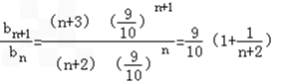 .当n=7时,
.当n=7时, 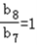 ,b8=b7;
,b8=b7;
当n<7时,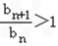 ,bn+1>bn;
,bn+1>bn;
当n>7时,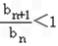 ,bn+1<bn.
,bn+1<bn.
∴当n=7或n=8时,bn取最大值,最大值为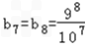 .
.
(3)解:由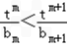 ,得
,得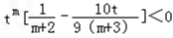 .(*)
.(*)
依题意,(*)式对任意m∈N*恒成立,
①当t=0时,(*)式显然不成立,因此t=0不合题意.
②当t<0时,由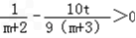 ,可知tm<0(m∈N*),而当m是偶数时tm>0,因此t<0不合题意.
,可知tm<0(m∈N*),而当m是偶数时tm>0,因此t<0不合题意.
③当t>0时,由tm>0(m∈N*),
∴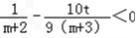 ,∴
,∴ 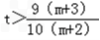 (m∈N*).
(m∈N*).
设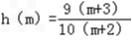 (m∈N*), ∵
(m∈N*), ∵ 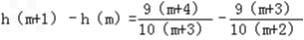 =
=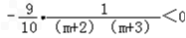 ,
,
∴h(1)>h(2)>…>h(m﹣1)>h(m)>….
∴h(m)的最大值为 .
.
所以实数t的取值范围是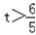 .
.
∴
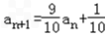 .
. ∴
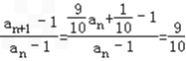 ,
,∵a1=2,
∴{an﹣1}是以a1﹣1=1为首项,公比为
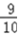 的等比数列.
的等比数列.(2)解:由( 1),可知an﹣1=
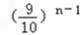 (n∈N*). ∴
(n∈N*). ∴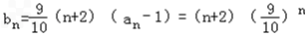 ,
,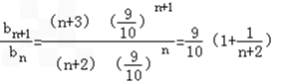 .当n=7时,
.当n=7时, 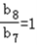 ,b8=b7;
,b8=b7;当n<7时,
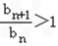 ,bn+1>bn;
,bn+1>bn;当n>7时,
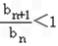 ,bn+1<bn.
,bn+1<bn. ∴当n=7或n=8时,bn取最大值,最大值为
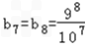 .
.(3)解:由
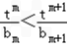 ,得
,得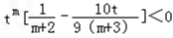 .(*)
.(*)依题意,(*)式对任意m∈N*恒成立,
①当t=0时,(*)式显然不成立,因此t=0不合题意.
②当t<0时,由
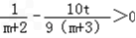 ,可知tm<0(m∈N*),而当m是偶数时tm>0,因此t<0不合题意.
,可知tm<0(m∈N*),而当m是偶数时tm>0,因此t<0不合题意.③当t>0时,由tm>0(m∈N*),
∴
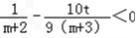 ,∴
,∴ 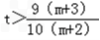 (m∈N*).
(m∈N*).设
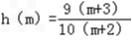 (m∈N*), ∵
(m∈N*), ∵ 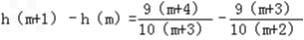 =
=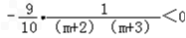 ,
, ∴h(1)>h(2)>…>h(m﹣1)>h(m)>….
∴h(m)的最大值为
 .
.所以实数t的取值范围是
 .
. 
练习册系列答案
相关题目