题目内容
设函数 ,其中ω是非零常数.
,其中ω是非零常数.
(1)若f(x)是增函数,则?的取值范围是________;
(2)若ω<0且f(x)的最大值为2,则?的最大值等于________.
解:(1)∵f(x)=2sinωx的最小正周期T=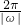 ,在[-
,在[- ,
, ]上是增函数所以ω>0
]上是增函数所以ω>0
又因为f(x)是增函数
? =
=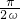 ≥
≥ ,解得0<ω≤
,解得0<ω≤ .
.
(2)∵函数f(x)=2sinωx在闭区间[- ,
, ]上的最大值是 2,
]上的最大值是 2,
所以sinωx的最大值为1,
当ω<0时,有- ≥
≥ ,得ω≤-2即ω≤-2.
,得ω≤-2即ω≤-2.
故?的最大值等于-2.
故答案为:- ≤ω<0或0<ω≤
≤ω<0或0<ω≤ ;-2.
;-2.
分析:(1)先求出函数的最小正周期,得到其增区间,再与条件相结合即可求出?的取值范围;
(2)根据函数有最大值2得到sinωx的最大值为1;再根据自变量的取值范围求出?的最大值即可.
点评:本题是基础题,考查三角函数的基本性质的应用,函数的单调性的应用,考查计算能力.
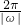 ,在[-
,在[- ,
, ]上是增函数所以ω>0
]上是增函数所以ω>0又因为f(x)是增函数
?
 =
=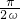 ≥
≥ ,解得0<ω≤
,解得0<ω≤ .
.(2)∵函数f(x)=2sinωx在闭区间[-
 ,
, ]上的最大值是 2,
]上的最大值是 2,所以sinωx的最大值为1,
当ω<0时,有-
 ≥
≥ ,得ω≤-2即ω≤-2.
,得ω≤-2即ω≤-2.故?的最大值等于-2.
故答案为:-
 ≤ω<0或0<ω≤
≤ω<0或0<ω≤ ;-2.
;-2.分析:(1)先求出函数的最小正周期,得到其增区间,再与条件相结合即可求出?的取值范围;
(2)根据函数有最大值2得到sinωx的最大值为1;再根据自变量的取值范围求出?的最大值即可.
点评:本题是基础题,考查三角函数的基本性质的应用,函数的单调性的应用,考查计算能力.

练习册系列答案
相关题目
 ,其中
,其中 是非零向量,则“函数f(x)的图象是一条直线”的充分条件是( )
是非零向量,则“函数f(x)的图象是一条直线”的充分条件是( )



 ,其中
,其中 是非零向量,则“函数f(x)的图象是一条直线”的充分条件是( )
是非零向量,则“函数f(x)的图象是一条直线”的充分条件是( )



 ,其中
,其中 是非零向量,则“函数f(x)的图象是一条直线”的充分条件是( )
是非零向量,则“函数f(x)的图象是一条直线”的充分条件是( )



 ,其中
,其中 是非零向量,则“函数f(x)的图象是一条直线”的充分条件是( )
是非零向量,则“函数f(x)的图象是一条直线”的充分条件是( )



 ,其中ω是非零常数.
,其中ω是非零常数.