题目内容
已知当|x|很小的时候,标准正态分布密度函数f(x)=
e-
可用函数g(x)=
(1-
)近似,若随机变量ξ服从标准正态分布,则下列说法中正确的是 .
①当x1>0时,有p(-x1≤ξ≤x1)=2p(0≤ξ≤x1);<BR②当
②当x1>x2>0 时,有p(ξ≥x2)>1-p(ξ≤x1);
③当|x1|,|x2|很小且x1<x2 时,有p(x1≤ξ≤x2)≈
[(x2-
)-x1-
)];
④当|x1|,|x2|很小且x1<x2 时,有p(x1≤ξ<x2)≈
(x1-x2).
| 1 | ||
|
| x2 |
| 2 |
| 1 | ||
|
| x2 |
| 2 |
①当x1>0时,有p(-x1≤ξ≤x1)=2p(0≤ξ≤x1);<BR②当
②当x1>x2>0 时,有p(ξ≥x2)>1-p(ξ≤x1);
③当|x1|,|x2|很小且x1<x2 时,有p(x1≤ξ≤x2)≈
| 1 | ||
|
| ||
| 6 |
| ||
| 6 |
④当|x1|,|x2|很小且x1<x2 时,有p(x1≤ξ<x2)≈
| 1 | ||
|
分析:根据ξ服从正态分布,先将标准正态分布密度函数转化成函数g(x)=
(1-
)近似,最后利用g(x)的图象与性质计算来表示出概率即可.
| 1 | ||
|
| x2 |
| 2 |
解答: 解:先作出g(x)的图象,如图.
解:先作出g(x)的图象,如图.
对于①由于分布密度函数关于y轴对称,故当x1>0时,有p(-x1≤ξ≤x1)=2p(0≤ξ≤x1);
得①正确;
对于②由于分布密度函数与x轴所围成的面积为1,故有:当x1>x2>0 时,有p(ξ≥x2)>1-p(ξ≤x1);得②正确;
对于③当|x1|,|x2|很小且x1<x2 时,
可得p(x1≤ξ≤x2)≈
[(x2-
)-x1+
)],故原式不能成立,③不正确;
对于④,当|x1|,|x2|很小且x1<x2 时,式子p(x1≤ξ<x2)≈
(x1-x2)不成立,故④不正确.
故答案为:①②
 解:先作出g(x)的图象,如图.
解:先作出g(x)的图象,如图.对于①由于分布密度函数关于y轴对称,故当x1>0时,有p(-x1≤ξ≤x1)=2p(0≤ξ≤x1);
得①正确;
对于②由于分布密度函数与x轴所围成的面积为1,故有:当x1>x2>0 时,有p(ξ≥x2)>1-p(ξ≤x1);得②正确;
对于③当|x1|,|x2|很小且x1<x2 时,
可得p(x1≤ξ≤x2)≈
| 1 | ||
|
| ||
| 6 |
| ||
| 6 |
对于④,当|x1|,|x2|很小且x1<x2 时,式子p(x1≤ξ<x2)≈
| 1 | ||
|
故答案为:①②
点评:本小题主要考查正态分布曲线的特点及曲线所表示的意义等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
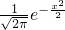 可用函数g(x)=
可用函数g(x)= 近似,若随机变量ξ服从标准正态分布,则下列说法中正确的是________.
近似,若随机变量ξ服从标准正态分布,则下列说法中正确的是________. ;
; .
.