题目内容
(本小题满分12分)如图,已知四棱锥 ,底面
,底面 为菱形,
为菱形, ⊥平面
⊥平面 ,
, ,
, 、
、 分别是
分别是 、
、 的中点。
的中点。
(Ⅰ)证明: ⊥
⊥ ;
;
 (Ⅱ)若
(Ⅱ)若 为
为 上的动点,
上的动点, 与平面
与平面 所成最大角的正切值为
所成最大角的正切值为 ,求二面角
,求二面角 的余弦值。
的余弦值。
.COM
【答案】
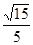
【解析】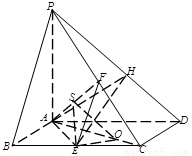 (Ⅰ)证明:由四边形
(Ⅰ)证明:由四边形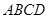 为菱形,
为菱形,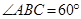 ,
,
可得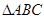 为正三角形。因为
为正三角形。因为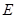 为
为 的中点,所以
的中点,所以 。 …………1分
。 …………1分
又 ∥
∥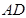 ,因此
,因此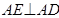 。…………………………………………………2分
。…………………………………………………2分
因为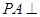 平面
平面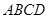 ,
,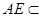 平面
平面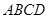 ,所以
,所以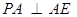 。 ………3分
。 ………3分
而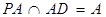 ,所以
,所以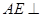 平面
平面 。 ………………………………4分
。 ………………………………4分
又 平面
平面 ,所以
,所以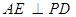 。 ……………………………………5分
。 ……………………………………5分
(Ⅱ)解:设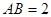 ,
,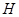 为
为 上任意一点,连接
上任意一点,连接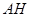 、
、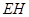
由(Ⅰ)可知: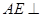 平面
平面 ,
,
则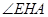 为
为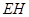 与平面
与平面 所成的角。……………………………………………6分
所成的角。……………………………………………6分
在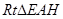 中,
中,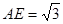 ,
,
所以当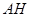 最短时,
最短时,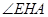 最大, ………………………………………………7分
最大, ………………………………………………7分
即当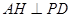 时,
时,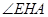 最大,此时
最大,此时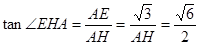 。www.7caiedu.cn
。www.7caiedu.cn
因此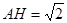 。又
。又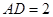 ,所以
,所以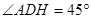 ,于是
,于是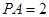 。 ……………………8分
。 ……………………8分
因为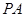 ⊥平面
⊥平面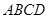 ,
,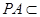 平面
平面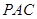 ,
,
所以平面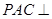 平面
平面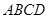 。 …………………………………………9分
。 …………………………………………9分
过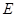 作
作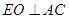 于
于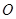 ,则由面面垂直的性质定理可知:
,则由面面垂直的性质定理可知: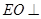 平面
平面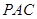 ,
,
过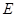 作
作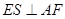 于
于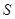 ,连接
,连接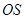 ,
,
则由三垂线定理可知: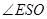 为二面角
为二面角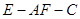 的平面角。 ……………………10分
的平面角。 ……………………10分
在 中,
中,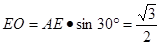 ,
,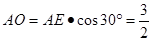
又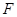 是
是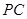 的中点,在
的中点,在 中,
中, www.7caiedu.cn
www.7caiedu.cn
又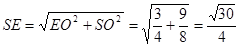 ………………………………11分
………………………………11分
在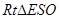 中,
中,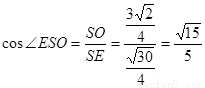
即二面角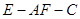 的余弦值为
的余弦值为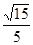 。 ………………………………12分
。 ………………………………12分

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目