Question

18．在平行四边形ABCD中，AB=4，AD=2，E，F分别是BC，CD的中点，且$\overrightarrow{DE}•\overrightarrow{BF}$=-15，则∠ABC=60°．

Answer 1

分析 以$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，表示$\overrightarrow{DE}$=$\overrightarrow{a}$$-\frac{1}{2}\overrightarrow{b}$，$\overrightarrow{BF}$=$\overrightarrow{b}$$-\frac{1}{2}\overrightarrow{a}$，运用数量积求解得出cos∠DAB=$-\frac{1}{2}$，即可求解∠DAB=120°，利用互补可求解．

解答 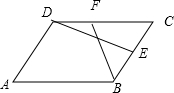解：设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，
∵AB=4，AD=2，E，F分别是BC，CD的中点，
∴$\overrightarrow{DE}$=$\overrightarrow{a}$$-\frac{1}{2}\overrightarrow{b}$，$\overrightarrow{BF}$=$\overrightarrow{b}$$-\frac{1}{2}\overrightarrow{a}$，
$\overrightarrow{DE}•\overrightarrow{BF}$=（$\overrightarrow{a}$$-\frac{1}{2}\overrightarrow{b}$）（$\overrightarrow{b}$$-\frac{1}{2}\overrightarrow{a}$）=$\overrightarrow{a}$$•\overrightarrow{b}$-10=-15，
即cos∠DAB=$-\frac{1}{2}$，
即∠ABC=180°-120°=60°
故答案为：60°

点评 本题考察了平行四边形的几何性质，平面向量的运算，属于容易题，关键是运用基底统一表示向量即可．