题目内容
已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,BD与α所成的角是30°,如果AB=3,AC=BD=4,D在平面α上的射影为D′,如图,求:(1)线段AC与BD所成的角;
(2)线段CD的长;
(3)二面角C—BD—D′的余弦值.
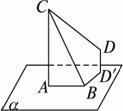
解:(1)∵D在α上的射影为D′
∴DD′⊥α.
又∵AC⊥α,∴AC∥DD′.
即AC与BD所成的角就是BD与DD′所成的角.
由题意,在Rt△DD′B中,∠BDD′=60°
∴线段AC与BD所成的角为60°.
(2)在Rt△DD′B中,BD′=2![]() ,DD′=2,
,DD′=2,
连结AD′,可证∠ABD′=90°,得AD′=![]() ,
,
取AC中点E,可证DE∥D′A,
在Rt△CED中,CD=![]() =5,即CD=5.
=5,即CD=5.
(3)连结CB,在Rt△CAB中,CB=5.
在等腰三角形CBD中取BD中点F,
则FC⊥BD,在△BDD′中过F作FH⊥BD交BD于H,
连结CH,则∠CFH就是面CBD与面BDD′所成的角,
在Rt△BFH中,得FH=![]() ,BH=
,BH=![]() ,
,
连结AH,得AH=![]() ,
,
在Rt△CAH中,CH=![]() ;在△CFH中,
;在△CFH中,
cosCFH=![]() ,
,
∴所求角的余弦值为![]() .
.

练习册系列答案
相关题目
