题目内容
已知曲线y= x3+
x3+ .
.
(1)求曲线在x=2处的切线方程;
(2)求曲线过点(2,4)的切线方程.
 x3+
x3+ .
. (1)求曲线在x=2处的切线方程;
(2)求曲线过点(2,4)的切线方程.
解:(1)∵P(2,4)在曲线 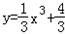 上,且y'=x2
上,且y'=x2
∴在点P(2,4)处的切线的斜率k=y'|x=2=4;
∴曲线在点P(2,4)处的切线方程为y﹣4=4(x﹣2),即4x﹣y﹣4=0.
(2)设曲线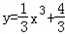 与过点P(2,4)的切线相切于点A(x0,
与过点P(2,4)的切线相切于点A(x0,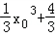 ),
),
则切线的斜率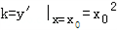 ,
,
∴切线方程为y﹣(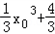 )=x02(x﹣x0),即
)=x02(x﹣x0),即 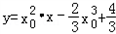
∵点P(2,4)在切线上,
∴4=2x02﹣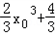 ,即x03﹣3x02+4=0,
,即x03﹣3x02+4=0,
∴x03+x02﹣4x02+4=0,
∴(x0+1)(x0﹣2)2=0
解得x0=﹣1或x0=2
故所求的切线方程为4x﹣y﹣4=0或x﹣y+2=0.
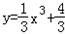 上,且y'=x2
上,且y'=x2∴在点P(2,4)处的切线的斜率k=y'|x=2=4;
∴曲线在点P(2,4)处的切线方程为y﹣4=4(x﹣2),即4x﹣y﹣4=0.
(2)设曲线
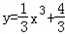 与过点P(2,4)的切线相切于点A(x0,
与过点P(2,4)的切线相切于点A(x0,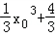 ),
),则切线的斜率
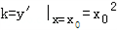 ,
,∴切线方程为y﹣(
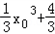 )=x02(x﹣x0),即
)=x02(x﹣x0),即 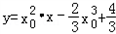
∵点P(2,4)在切线上,
∴4=2x02﹣
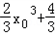 ,即x03﹣3x02+4=0,
,即x03﹣3x02+4=0,∴x03+x02﹣4x02+4=0,
∴(x0+1)(x0﹣2)2=0
解得x0=﹣1或x0=2
故所求的切线方程为4x﹣y﹣4=0或x﹣y+2=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目