题目内容

如果点P在平面区域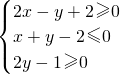 $数学公式$ 上，点Q在曲线x²+（y+3）²=1上，那么|PQ|的最小值为________．

$\text{[math]}$
分析：作出可行域，将|PQ|的最小值转化为圆心到可行域的最小值，结合图形，求出|CP|的最小值，减去半径得PQ|的最小值．
解答：

解：作出可行域，要使|PQ|的最小，
只要圆心C（0，-3）到P的距离最小，
结合图形当P（0， $\text{[math]}$ ）时，|CP|最小为 $\text{[math]}$
又因为圆的半径为1
故|PQ|的最小为 $\text{[math]}$ = $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本题属于线性规划中的延伸题，对于可行域不要求线性目标函数的最值，而是求可行域内的点与（0，-3）之间的距离问题