题目内容
6.已知f(α)=$\frac{{cos({3π+α})cos({\frac{3π}{2}+α})sin({-α})}}{{tan({-π-α})sin({3π-α})cos({-π-α})}}$.(1)化简f(α);
(2)已知角α为锐角,$f({α+\frac{π}{6}})=\frac{3}{5}$,求f(α)的值.
分析 (1)运用诱导公式及同角三角函数基本关系的运用即可化简得解.
(2)利用已知可得cos($α+\frac{π}{6}$)=$\frac{3}{5}$且$α+\frac{π}{6}$∈($\frac{π}{6}$,$\frac{2π}{3}$),根据同角三角函数基本关系的运用可求sin($α+\frac{π}{6}$)的值,从而利用两角差的余弦函数公式即可求得f(α)=cosα=cos($α+\frac{π}{6}-\frac{π}{6}$)的值.
解答 解:(1)f(α)=$\frac{{cos({3π+α})cos({\frac{3π}{2}+α})sin({-α})}}{{tan({-π-α})sin({3π-α})cos({-π-α})}}$
=$\frac{(-cosα)sinα(-sinα)}{(-tanα)sinα(-cosα)}$
=cosα.
(2)∵角α为锐角,$f({α+\frac{π}{6}})=\frac{3}{5}$,cos($α+\frac{π}{6}$)=$\frac{3}{5}$
∴$α+\frac{π}{6}$∈($\frac{π}{6}$,$\frac{2π}{3}$),
∴sin($α+\frac{π}{6}$)=$\sqrt{1-co{s}^{2}(α+\frac{π}{6})}$=$\frac{4}{5}$,
∴f(α)=cosα=cos($α+\frac{π}{6}-\frac{π}{6}$)=cos($α+\frac{π}{6}$)cos$\frac{π}{6}$+sin($α+\frac{π}{6}$)sin$\frac{π}{6}$=$\frac{3}{5}×\frac{\sqrt{3}}{2}+\frac{4}{5}×\frac{1}{2}$=$\frac{3\sqrt{3}+4}{10}$.
点评 本题主要考查了同角三角函数基本关系的运用,运用诱导公式化简求值,属于基本知识的考查.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 2016×2 017 | B. | 2015×2 016 | C. | 2014×2 015 | D. | 2016×2 016 |
| A. | 不能作出满足要求的三角形 | B. | 作出一个钝角三角形 | ||
| C. | 作出一个直角三角形 | D. | 作出一个锐角三角形 |
| A. | “b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件. | |
| B. | 命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” | |
| C. | 命题“在△ABC中,若A>B则sinA>sinB”的逆命题为假命题. | |
| D. | 函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件. |
| 篮球 | 排球 | 总计 | |
| 男同学 | 16 | 6 | 22 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
(下面临界值表供参考
| P(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| A. | 99% | B. | 95% | C. | 90% | D. | 无关系 |
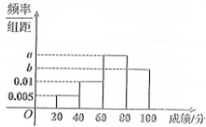 某班的全体学生(共50人)参加数学测试(百分制),成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],依此表可以估计这次测试成绩的中位数为70分.
某班的全体学生(共50人)参加数学测试(百分制),成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],依此表可以估计这次测试成绩的中位数为70分.