题目内容
如图,线段PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12,△ACF的面积为72,求△BDE的面积.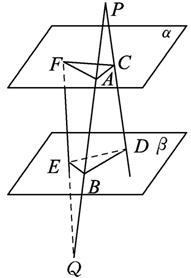
解析:平面QAF∩α=AF,平面QAF∩β=BE,
又∵α∥β,∴AF∥BE.
同理可证:AC∥BD,∴∠FAC与∠EBD相等或互补,
即sin∠FAC=sin∠EBD.
由FA∥BE,得BE:AF:AF=QB:QA=12:24=1:2,
∴BE=![]() AF.
AF.
由BD∥AC,得:AC:BD=PA:PB=9:21=3:7,
∴BD=![]() AC.
AC.
又∵△ACF的面积为72,即1[]2AF·AC·sin∠FAC=72.
∴S△DBE=![]() BE·BD·sin∠EBD
BE·BD·sin∠EBD
=![]() ·
·![]() AF·
AF·![]() AC·sin∠FAC
AC·sin∠FAC
=![]() AF·AC·sin∠FAC=
AF·AC·sin∠FAC=![]() ×72=84.
×72=84.
∴△BDE的面积为84.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目

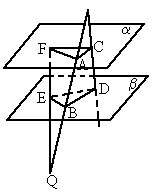
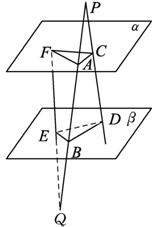
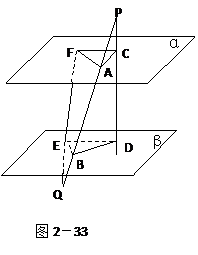 如图2-33:线段PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12,
如图2-33:线段PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12,