题目内容
 如图,在梯形ABCD中,DA=AB=BC=
如图,在梯形ABCD中,DA=AB=BC=| 1 |
| 2 |
| AP |
| BD |
[-
,
]
| 3 |
| 2 |
| 3 |
| 2 |
[-
,
]
.| 3 |
| 2 |
| 3 |
| 2 |
分析:建立平面直角坐标系,将
•
的取值范围的求解,转化为利用线性规划的方法解决即可.
| AP |
| BD |
解答:解:以点A为坐标原点,AB为x轴,过点A垂直于AB的直线为y轴,建立如图所示的坐标系,
 则A(0,0),B(1,0),C(
则A(0,0),B(1,0),C(
,
),D(-
,
),
设点P的坐标为(x,y),
则
•
=(x,y)(-
,
)=-
x+
y,
令z=-
x+
y,而直线BD的方程为:x+
y-
=0,
直线BC的方程为:
x-y-
=0,
当z=-
x+
y过点D时z取最大值
,过BC线段上任意一点时z取最小值-
,
∴
•
的取值范围是:[-
,
].
故答案为:[-
,
].
 则A(0,0),B(1,0),C(
则A(0,0),B(1,0),C(| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
设点P的坐标为(x,y),
则
| AP |
| BD |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
令z=-
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
直线BC的方程为:
| 3 |
| 3 |
当z=-
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴
| AP |
| BD |
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:[-
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题主要考查了取值范围的确定,考查数形结合的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
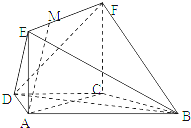 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.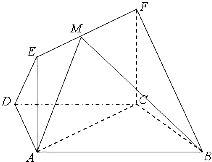 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.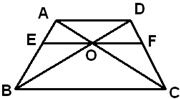 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.