题目内容
函数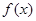 的定义域为
的定义域为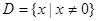 ,且满足对于任意
,且满足对于任意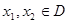 ,有
,有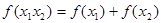 .
.
⑴求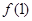 的值;
的值;
⑵判断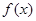 的奇偶性并证明;
的奇偶性并证明;
⑶如果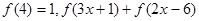 ≤
≤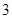 ,且
,且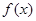 在
在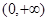 上是增函数,求
上是增函数,求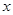 的取值范围.
的取值范围.
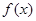 的定义域为
的定义域为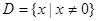 ,且满足对于任意
,且满足对于任意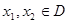 ,有
,有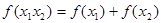 .
.⑴求
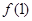 的值;
的值;⑵判断
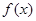 的奇偶性并证明;
的奇偶性并证明;⑶如果
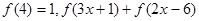 ≤
≤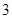 ,且
,且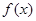 在
在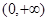 上是增函数,求
上是增函数,求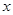 的取值范围.
的取值范围.⑴令 ,则
,则
 .
.
⑵令 ,则
,则
 ,
,
再令
 ,则
,则 ,故函数
,故函数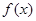 为偶函数.
为偶函数.
⑶由 ,可得
,可得 ,
,

 在
在 单调递增,
单调递增, 单调递减
单调递减
 且
且 且
且

∴
 ,则
,则
 .
. ⑵令
 ,则
,则
 ,
,再令

 ,则
,则 ,故函数
,故函数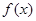 为偶函数.
为偶函数.⑶由
 ,可得
,可得 ,
,
 在
在 单调递增,
单调递增, 单调递减
单调递减 且
且 且
且

∴

(Ⅰ) 通过赋值法, ,求出f(1)0;
,求出f(1)0;
(Ⅱ) 说明函数f(x)的奇偶性,通过令 ,得
,得 .令
.令
 ,得
,得 ,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.
,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.
(Ⅲ) 推出函数的周期,根据函数在[-2,2]的图象以及函数的周期性,即可求满足f(2x-1)≥12的实数x的集合.
 ,求出f(1)0;
,求出f(1)0;(Ⅱ) 说明函数f(x)的奇偶性,通过令
 ,得
,得 .令
.令
 ,得
,得 ,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.
,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.(Ⅲ) 推出函数的周期,根据函数在[-2,2]的图象以及函数的周期性,即可求满足f(2x-1)≥12的实数x的集合.

练习册系列答案
相关题目
 且
且 .
.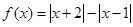 .
.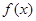 的值域;
的值域;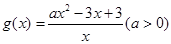 ,若对
,若对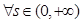 ,
, 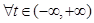 ,恒
,恒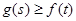 成立,试求实数
成立,试求实数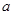 的取值范围
的取值范围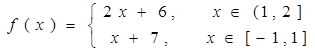 则
则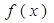 的最大值,最小值分别为( ).
的最大值,最小值分别为( ).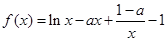
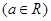 .
.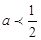 时,讨论
时,讨论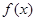 的单调性;
的单调性;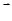
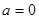 时,对于任意的
时,对于任意的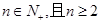 ,证明:不等式
,证明:不等式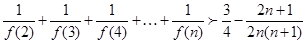
 的函数
的函数 若关于x的方程
若关于x的方程 有7个不同的实数解,则
有7个不同的实数解,则 =( )
=( )
 是
是 上的减函数。那么
上的减函数。那么 的取值范围是
的取值范围是



 则
则 的值是 ___
的值是 ___ 的值等于___________。
的值等于___________。