题目内容
给出下面关系式:(1)0•| a |
| a |
| b |
| b |
| a |
| a |
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
分析:因为零向量与任意向量的数量积为0,得到(1)是错误的;根据向量数量积的定义知(2)正确,根据向量数量积的运算律知(3)正确,数量积不符合结合律,故(4)错误,两个向量数量积的绝对值大于或等于两个向量的数量积,故(5)错误,
解答:解:(1)是错误的,因为零向量与任意向量的数量积为0,
根据向量数量积的定义知(2)正确,
根据向量数量积的运算律知(3)正确,
数量积不符合结合律,故(4)错误,
两个向量数量积的绝对值大于或等于两个向量的数量积,故(5)错误,
综上所述(2)(3)正确,
故答案为:(2)(3)
根据向量数量积的定义知(2)正确,
根据向量数量积的运算律知(3)正确,
数量积不符合结合律,故(4)错误,
两个向量数量积的绝对值大于或等于两个向量的数量积,故(5)错误,
综上所述(2)(3)正确,
故答案为:(2)(3)
点评:本题考查两个向量数量积的性质,考查向量数量积的运算律,是一个概念辨析问题,解这种题目的关键是正确理解数量积的概念.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 ;(2)
;(2)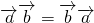 ;(3)
;(3) ;(4)
;(4) ;(5)
;(5) ,其中正确的序号是 ________.
,其中正确的序号是 ________.