题目内容
 如图所示,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上二点P的位置在(0,0),圆在x轴上沿正向滚动,则当圆滚动到圆心位于(2,1)时线段OP与初始单位圆的交点为M,则|OM|=
如图所示,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上二点P的位置在(0,0),圆在x轴上沿正向滚动,则当圆滚动到圆心位于(2,1)时线段OP与初始单位圆的交点为M,则|OM|=| 2-2cos2 | ||
|
| 2-2cos2 | ||
|
分析:求单位圆中的弦长,关键是求出α的三角函数值,确定P的坐标即可.
解答:解:设∠xOP=α,N(0,1),连接MN,则∠ONM=2α
∵圆滚动了2单位个弧长,点P旋转了2弧度,
∴P(2-sin2,1-cos2),
∴|OP|=
=
∴sinα=
在△ONM中,|OM|=2|MN|sinα=2sinα=
故答案为:
∵圆滚动了2单位个弧长,点P旋转了2弧度,
∴P(2-sin2,1-cos2),
∴|OP|=
| (2-sin2)2+(1-cos2)2 |
| 6-4sin2-2cos2 |
∴sinα=
| 1-cos2 | ||
|
在△ONM中,|OM|=2|MN|sinα=2sinα=
| 2-2cos2 | ||
|
故答案为:
| 2-2cos2 | ||
|
点评:本题考查三角函数的定义,考查学生的计算能力,确定P的坐标是关键.

练习册系列答案
相关题目
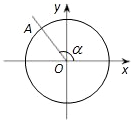 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为 (2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m. 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为