题目内容
(本小题满分13分)如图,已知三棱柱 的所有棱长都相等,且侧棱垂直于底面,由
的所有棱长都相等,且侧棱垂直于底面,由 沿棱柱侧面经过棱
沿棱柱侧面经过棱 到点
到点 的最短路线长为
的最短路线长为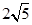 ,设这条最短路线与
,设这条最短路线与 的交点为
的交点为 .
.
(1)求三棱柱 的体积;
的体积;
(2)在面 内是否存在过
内是否存在过 的直线与面
的直线与面 平行?证明你的判断;
平行?证明你的判断;
(3)证明:平面 ⊥平面
⊥平面 .
.
【答案】

平面A1BD内存在过点D的直线与平面ABC平行.
【解析】解:(1)如图,将侧面BB1C1C绕棱CC1旋转120°,
使其与侧面AA1C1C在同一平面上,点B运动到
点B2的位置,连接A1B2,则A1B2就是由点B沿
棱柱侧面经过棱CC1到点A1的最短路线.
设棱柱的棱长为 ,则B2C=AC=AA1=
,则B2C=AC=AA1= ,
,
∵CD∥AA1 , ∴ 为
为 的中点.
………2分
的中点.
………2分
在Rt△A1AB2中,由勾股定理得 ,
,
即 ,解得
,解得 ,
∵
,
∵ ,
,
∴ .
………5分
.
………5分
(2)设A1B与AB1的交点为O,连结BB2,OD,则 .
.
∵ 平面
平面 ,
, 平面
平面 , ∴
, ∴ 平面
平面 ,
,
即在平面A1BD内存在过点D的直线与平面ABC平行. ………9分
(3)连结AD,B1D ∵ ≌
≌ ≌
≌ ≌
≌ ,
,
∴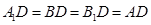 , ∴
, ∴ .
.
∵ ,
, ,
,
∴ 平面A1ABB1 ,又∵
平面A1ABB1 ,又∵ 平面A1BD.
平面A1BD.
∴平面A1BD⊥平面A1ABB1 . ………13分

练习册系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和