题目内容
由函数![]() 确定数列
确定数列![]() ,
,![]() ,函数
,函数![]() 的反函数
的反函数![]() 能确定数列
能确定数列![]() ,
,![]() ,若对于任意
,若对于任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 是数列
是数列![]() 的“自反数列”。
的“自反数列”。
(1)若函数![]() 确定数列
确定数列![]() 的自反数列为
的自反数列为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)在(1)条件下,记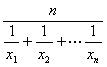 为正数数列
为正数数列![]() 的调和平均数,若
的调和平均数,若![]() ,
,
![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() 为数列
为数列![]() 的调和平均数,求
的调和平均数,求![]() ;
;
(3)已知正数数列![]() 的前
的前![]() 项之和
项之和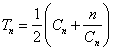 。求
。求![]() 的表达式。
的表达式。
解 (1) 由题意的:f –1(x)=![]() = f(x)=
= f(x)=![]() ,所以p = –1,所以an=
,所以p = –1,所以an=![]()
(2) an=![]() ,dn=
,dn=![]() =n,
=n,
Sn为数列{dn}的前n项和,Sn=![]() ,又Hn为数列{Sn}的调和平均数,
,又Hn为数列{Sn}的调和平均数,
Hn= =
= =
=![]()
![]() =
=![]() =
=![]()
(3) 因为正数数列{cn}的前n项之和Tn=![]() (cn+
(cn+![]() ),
),
所以c1=![]() (c1+
(c1+![]() ),解之得:c1=1,T1=1
),解之得:c1=1,T1=1
当n≥2时,cn = Tn–Tn–1,所以2Tn = Tn–Tn–1 +![]() ,
,
Tn +Tn–1 = ![]() ,即:
,即:![]() = n,
= n,
所以,![]() = n–1,
= n–1,![]() = n–2,……,
= n–2,……,![]() =2,累加得:
=2,累加得:
![]() =2+3+4+……+ n,
=2+3+4+……+ n, ![]() =1+2+3+4+……+ n =
=1+2+3+4+……+ n =![]() ,Tn=
,Tn=![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 ,写出
,写出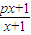 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+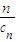 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;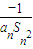 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围. ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+ ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论; ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.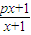 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+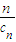 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;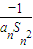 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.