题目内容
成都某中学2011年进行评定高级职称工作时,数学组、语文组各有2人够资格,能评上高级职称的可能性分别为
和
,且每个人是否评上互不影响.
(I)求这两个组至少有1人评上的概率;
(II)求数学组评上的人数ξ的期望和方差.
| 2 |
| 3 |
| 1 |
| 2 |
(I)求这两个组至少有1人评上的概率;
(II)求数学组评上的人数ξ的期望和方差.
设Ak表示数学组评上k人(k=0,1,2),设Bi表示语文组评上i人(i=0,1,2).
P(Ak)=
(
)k(
)2-k,P(Bi)=
(
)i(
)2-i=
(
)2.
(I)P=1-P(A0•B0)=1-P(A0)•P(B0)=1-(
)2(
)2=
;
(II)由题意ξ~B(2,
)
∴期望Eξ=2×
=
,方差Dξ=2×
×
=
,
答:(I)这两个组至少有1人评上的概率是
;
(II)数学组评上的人数ξ的期望Eξ=2×
=
,方差Dξ=2×
×
=
.
P(Ak)=
| C | k2 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | i2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | i2 |
| 1 |
| 2 |
(I)P=1-P(A0•B0)=1-P(A0)•P(B0)=1-(
| 1 |
| 3 |
| 1 |
| 2 |
| 35 |
| 36 |
(II)由题意ξ~B(2,
| 2 |
| 3 |
∴期望Eξ=2×
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
答:(I)这两个组至少有1人评上的概率是
| 35 |
| 36 |
(II)数学组评上的人数ξ的期望Eξ=2×
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 和
和 ,且每个人是否评上互不影响.
,且每个人是否评上互不影响.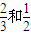 ,且每个人是否评上互不影响.
,且每个人是否评上互不影响.