题目内容
给出三个电器元件，已知每个电器元件损坏的概率为p，按照图(1)、(2)两种不同的方法联接到线路中，试求(1)、(2)两种线路正常工作的概率.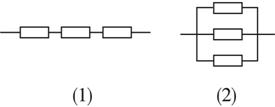
思路解析：(1)中只有3个元件是串联在线路中，只有3个元件都没有损坏，线路才能正常工作；(2)中3个元件是并联在线路中，3个元件中至少有1个没有损坏，线路就能正常工作.
(1)解：“线路能正常工作”的概率为(1－p)3.
(2)解法一：“3个元件中有1个没有损坏”的概率
p2(1－p)1；“3个元件中有2个没有损坏”的概率
p(1－p)2；“3个元件都没有损坏”的概率为
(1－p)3，所以线路能正常工作的概率为3个元件至少有1个没有损坏的概率，即为
p2(1－p)1+
p(1－p)2+
(1－p)3=1－p3.
解法二：“3个元件中至少有1个没有损坏”的对立事件是“3个元件都被损坏”.
“一个元件被损坏”的概率为p，“3个元件都被损坏”的概率为p3，所以“3个元件中至少有1个没被损坏即线路能正常工作”的概率为1－p3.
练习册系列答案
相关题目