Question

（本小题满分12分）

   已知函数

   （1）证明：当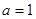时，函数只有一个零点；

   （2）若函数在区间（1，+∞）上是减函数，求实数的取值范围。

 

Answer 1

【答案】

（1）函数只有一个零点；    证明略

（2）实数a的取值范围是

【解析】解：（1）当a=1时，

其定义域为

    …………2分

解得

当，

在区间（0，1）上单调递增，

在区间上单调递减，

当x=1时，函数f（x）取得最大值，即    …………4分

所以函数只有一个零点；     …………5分

（2）因为，

所以

①当a=0时，

所以上为增函数，不合题意  …………7分

②当，

即，此时，f（x）的单调减区间为，依题意，

得       …………9分

   （3）当

即的单调减区间为

综上所述，实数a的取值范围是  …………12分