题目内容
(1)设x≥1,y≥1,证明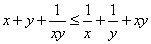 ;
;
(2)设1<a≤b≤c,证明logab+logbc+logca≤logba+ logcb+logac。
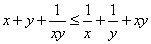 ;
;(2)设1<a≤b≤c,证明logab+logbc+logca≤logba+ logcb+logac。
解:(1)由于x≥1,y≥1,所以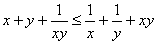
 xy(x+y)+1≤y+x+(xy)2
xy(x+y)+1≤y+x+(xy)2
将上式中的右式减左式,得(y+x+(xy)2)-(xy(x+y)+1)
=((x+y)2-1)-(xy(x+y)-(x+y))
=(xy+1)(xy-1)-(x+y)(xy-1)
=(xy-1)(xy-x-y+1)
=(xy-1)(x-1)(y-1)
既然x≥1,y≥1,所以(xy-1)(x-1)(y-1)≥0,从而所要证明的不等式成立。
(2)设logab=x,logbc=y,由对数的换底公式得,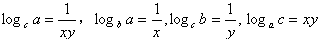
于是,所要证明的不等式即为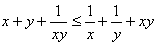
其中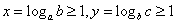
故由(1)知所要证明的不等式成立。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知0<a<b<1,设x=logb
,y=loga
,z=logab,则( )
| 1 |
| b |
| 1 |
| b |
| A、y<x<z |
| B、y<z<x |
| C、x<z<y |
| D、x<y<z |
 已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下,抽出学生n人,成绩只有3、4、5三种分值,设x,y分别表示项目A与项目B成绩.例如:表中项目A成绩为5分的共7+9+4=20人.已知x=4且y=5的概率是0.2.
已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下,抽出学生n人,成绩只有3、4、5三种分值,设x,y分别表示项目A与项目B成绩.例如:表中项目A成绩为5分的共7+9+4=20人.已知x=4且y=5的概率是0.2.