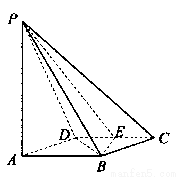
题目内容
 如图所示,四棱锥
如图所示,四棱锥![]() 的底面是边长为1的正方形,
的底面是边长为1的正方形,![]() ,
,![]() ,
,![]() 点是棱
点是棱![]() 的中点。
的中点。
(1)求证![]() ;
;
(2)求异面直线![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(3)求面![]() 与面
与面![]() 所成二面角的大小。
所成二面角的大小。
(第18题图)
见解析
解析:
解法一:
(1)因为![]() ,所以SC在底面的射影是CD
,所以SC在底面的射影是CD
又因为底面ABCD是正方形,所以![]() ,所以
,所以![]() …………4分
…………4分
(2)取AB的中点P,连结MP,DP
在![]() 中,由中位线得 MP//SB ,所以
中,由中位线得 MP//SB ,所以![]()
是异面直线DM与SB所成的角或其补角,
因为 ![]() ,又
,又![]() ,
,
 所以
所以![]() ,因此
,因此![]()
所以异面直线DM与SB所成的角为![]() …………9分
…………9分
(3)因为![]() ,底面ABCD是正方形,
,底面ABCD是正方形,
所以可以把四棱锥补成长方体![]() ,
,
面![]() 与面
与面![]() 所成二面角就是面
所成二面角就是面![]() 与面
与面![]() 所成二面角
所成二面角
因为![]() ,
,![]() ,所以
,所以![]()
又![]() ,所以
,所以![]() 为所求的二面角的平面角
为所求的二面角的平面角
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,在
,在![]() ,得
,得![]()
所以![]() ,即面
,即面![]() 与面
与面![]() 所成二面角为
所成二面角为![]() 。. …………14分
。. …………14分

解法二:以点D为坐标原点,建立如图的空间直角坐标系,
因为ABCD是边长为1的正方形,且![]() ,
,
所以![]() ,
,![]() ,则
,则 ![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]()
因为![]() ,
,![]() ,则
,则![]()
所以![]() ,即
,即![]() …………4分
…………4分
(2)设所求的异面直线所成的角为![]() ,因为
,因为![]()
![]()
所以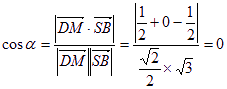
故异面直线DM与SB所成的角为![]() …………9分
…………9分
(3)设所求二面角的平面角为![]() ,由题意可以面ASD的一个法向量为
,由题意可以面ASD的一个法向量为![]() ,设面BSC的一个法向量为
,设面BSC的一个法向量为![]() ,则
,则
所以 ![]()
而![]() 与
与![]() 所成的角就是所求的二面角的平面角或其补角,所以
所成的角就是所求的二面角的平面角或其补角,所以
所以面![]() 与面
与面![]() 所成二面角为
所成二面角为![]() 。…………14分
。…………14分

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

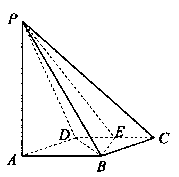


 的底面为直角梯形,
的底面为直角梯形, ,
, ,
, ,
, ,
, 底面
底面 ,
, 为
为 的中点.
的中点. 平面
平面 ;
; 与平面
与平面 所成的角;
所成的角; 到平面
到平面
 的底面
的底面 是边长为1的菱形,
是边长为1的菱形, ,
, 底面ABCD,
底面ABCD, 。
。