题目内容
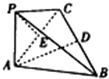 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=AC,∠BAC为直角,D,E分别为BC,AC的中点,AB=2PA.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=AC,∠BAC为直角,D,E分别为BC,AC的中点,AB=2PA.(1)BC上是否存在一点F,使AD∥平面PEF?请说明理由;
(2)对于(1)中的点F,求AF与平面PEF所成角的正弦值.
分析:(1)取CD的中点F,连接EF、PF,由三角形中位线定理,可得EF∥AD,再由线面平行的判定定理,可得AD∥平面PEF.
(2)设PA=1,则AB=AC=2,利用线面垂直的性质结合勾股定理,得到△PEF的各边长,再用正余弦定理算出其面积S△PEF=
.设A到平面PEF的距离为d,利用三棱锥的体积进行转换,即得d=
,最后根据线面所成角的性质,得到AF与平面PEF所成角θ满足sinθ=
=
,从而得到答案.
(2)设PA=1,则AB=AC=2,利用线面垂直的性质结合勾股定理,得到△PEF的各边长,再用正余弦定理算出其面积S△PEF=
| ||
| 4 |
| ||
| 3 |
| d |
| AF |
| ||
| 15 |
解答:解:(1)取CD的中点F,连接EF、PF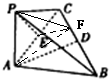
∵△ACD中,E、F分别为AC、CD的中点,
∴EF∥AD,且EF=
AD
∵EF⊆平面PEF,AD?平面PEF,
∴AD∥平面PEF,
所以存在CD的中点F,使AD∥平面PEF.
(2)设PA=1,则AB=AC=2
∵△ABC是以BC为斜边的直角三角形,AD是BC边的中线
∴BC=
,且AD=BD=CD=
BC=
Rt△ADF中,DF=
CD=
,可得AF=
=
∵PA⊥平面ABC,AF⊆平面ABC,
∴PA⊥AF,可得Rt△PAF中,PF=
=
同理可得Rt△PAE中,PE=
=
∴△PEF中,EF=
AD=
,可得cos∠EPF=
=
由同角三角函数关系,得sin∠EPF=
=
∴△EPF的面积S△EPF=
PE•PFsin∠EPF=
×
×
×
=
∵△EAF的面积S△EAF=
S△ADC=
∴三棱锥P-AEF的体积V=
×S△EAF×PA=
设A到平面PEF的距离为d,则VA-PEF=
×S△EPF×d=
即
d=
,可得d=
所以AF与平面PEF所成角θ满足sinθ=
=
∴AF与平面PEF所成角的正弦值等于

∵△ACD中,E、F分别为AC、CD的中点,
∴EF∥AD,且EF=
| 1 |
| 2 |
∵EF⊆平面PEF,AD?平面PEF,
∴AD∥平面PEF,
所以存在CD的中点F,使AD∥平面PEF.
(2)设PA=1,则AB=AC=2
∵△ABC是以BC为斜边的直角三角形,AD是BC边的中线
∴BC=
| 2 |
| 1 |
| 2 |
| 2 |
Rt△ADF中,DF=
| 1 |
| 2 |
| ||
| 2 |
| AD2+DF2 |
| ||
| 2 |
∵PA⊥平面ABC,AF⊆平面ABC,
∴PA⊥AF,可得Rt△PAF中,PF=
| AP2+AF2 |
| ||
| 2 |
同理可得Rt△PAE中,PE=
| AP2+AE2 |
| 2 |
∴△PEF中,EF=
| 1 |
| 2 |
| ||
| 2 |
| PE2+PF2-EF2 |
| 2PE•PF |
5
| ||
| 14 |
由同角三角函数关系,得sin∠EPF=
| 1-cos2∠EPF |
| ||
| 14 |
∴△EPF的面积S△EPF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 14 |
| ||
| 4 |
∵△EAF的面积S△EAF=
| 1 |
| 4 |
| 1 |
| 4 |
∴三棱锥P-AEF的体积V=
| 1 |
| 3 |
| 1 |
| 12 |
设A到平面PEF的距离为d,则VA-PEF=
| 1 |
| 3 |
| 1 |
| 12 |
即
| ||
| 4 |
| 1 |
| 4 |
| ||
| 3 |
所以AF与平面PEF所成角θ满足sinθ=
| d |
| AF |
| ||
| 15 |
∴AF与平面PEF所成角的正弦值等于
| ||
| 15 |
点评:本题给出底面是等腰直角三角形且一条侧棱与底面垂直的三棱锥,证明线面平行并求线面所成的角,着重考查了线面平行、垂直的判定与性质和直线与平面所成角等知识,属于中档题.

练习册系列答案
相关题目
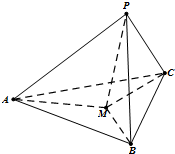 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=( 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( )
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( ) 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点. 如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是
如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是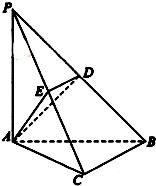 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱