题目内容
【题目】选修4-4:坐标系与参数方程
已知曲线![]() :
:  (
(![]() 为参数)和直线
为参数)和直线![]() :
: ![]() (
(![]() 为参数).
为参数).
(1)将曲线![]() 的方程化为普通方程;
的方程化为普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() 为弦
为弦![]() 的中点,求弦
的中点,求弦![]() 所在的直线方程.
所在的直线方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:熟悉万能代换公式的同学都知道,把曲线![]() 的方程化为普通方程的方法是换元,令
的方程化为普通方程的方法是换元,令![]() 消元更方便,当然本题也可直接消元,先求出
消元更方便,当然本题也可直接消元,先求出![]() 后分离常数,与
后分离常数,与![]() 相除,得出
相除,得出![]() ,再代入消元整理;第二步为直线的参数方程
,再代入消元整理;第二步为直线的参数方程![]() 的几何意义问题,代入参数方程整理为
的几何意义问题,代入参数方程整理为![]() 的一元二次方程,由于
的一元二次方程,由于![]() 为弦
为弦![]() 的中点,则
的中点,则![]() ,求出直线方程.
,求出直线方程.
试题解析:(1)由![]() ,得
,得![]() ,即
,即![]() ,又
,又![]() ,两式相除得
,两式相除得![]() ,代入
,代入![]() ,得
,得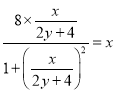 ,整理得
,整理得![]() ,即为
,即为![]() 的普通方程.
的普通方程.
(2)将![]() 代入
代入![]() ,
,
整理得![]() .由
.由![]() 为
为![]() 的中点,则
的中点,则![]() .
.
∴![]() ,即
,即![]() ,故
,故![]() ,即
,即![]() ,所以所求的直线方程为
,所以所求的直线方程为![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目