题目内容
设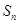 为等差数列
为等差数列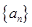 的前
的前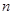 项和,已知
项和,已知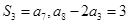 .
.
(1)求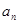 ;
;
(2)设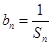 ,数列
,数列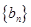 的前
的前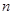 项和记为
项和记为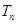 ,求证:
,求证: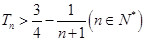 .
.
(1)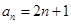 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)将题设代入等差数列的公式得方程组: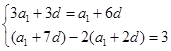 ,解这个方程组求出
,解这个方程组求出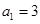 ,
,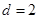 ,从而可得通项公式.(2)由(1)得,
,从而可得通项公式.(2)由(1)得,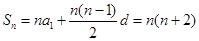 ,所以
,所以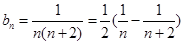 ,用裂项法求得
,用裂项法求得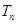
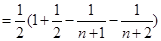 ,再用放缩法将
,再用放缩法将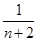 变为
变为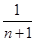 即得.
即得.
(1)设数列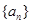 的公差为
的公差为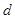 ,由题得
,由题得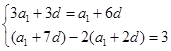 3分
3分
解得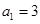 ,
,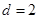 5分
5分
∴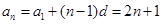 6分
6分
(2)由(1)得,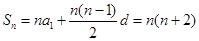 8分
8分
∴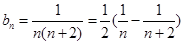 10分
10分
∴
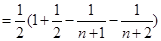 12分
12分
∴ 13分
13分
考点:1、等差数列;2、裂项法;3、不等式的证明.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
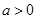 ,且
,且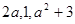 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值;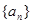 的首项和公差都为
的首项和公差都为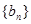 的首项和公比都为
的首项和公比都为 项和分别为
项和分别为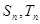 ,且
,且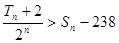 ,求满足条件的自然数
,求满足条件的自然数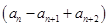 x+an+1cos x-an+2sin x满足f′
x+an+1cos x-an+2sin x满足f′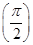 =0.
=0.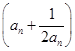 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.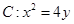 ,直线
,直线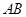 过抛物线
过抛物线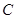 的焦点
的焦点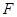 ,交
,交 轴于点
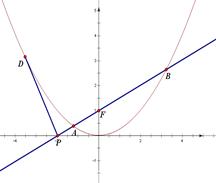
轴于点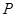 .
.
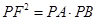 ;
;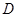 (异于原点),
(异于原点),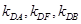 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;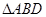 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.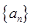 ,
,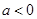 满足
满足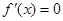 ,
,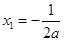 ,
,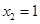 ,
,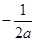 .
.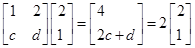 是等差数列,并求数列
是等差数列,并求数列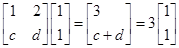 的通项公式;
的通项公式;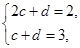 满足
满足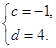 ,对于任意给定的正整数
,对于任意给定的正整数 ,是否存在正整数
,是否存在正整数 ,
, (
( ),使得
),使得 ,
,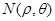 ,
,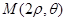 成等差数列?若存在,试用
成等差数列?若存在,试用 表示
表示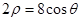 ;若不存在,说明理由.
;若不存在,说明理由.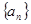 是等差数列,且
是等差数列,且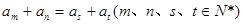 ,
,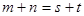 ;
;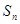 是等差数列
是等差数列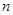 项的和,则
项的和,则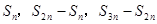 成等差数列;
成等差数列;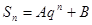 ;(其中
;(其中 是非零常数,
是非零常数,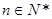 ),则
),则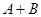 为零.
为零. ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: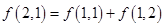 ;
;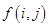 为数表中第
为数表中第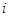 行的第
行的第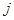 个数.
个数.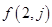 和
和 ;
;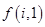 关于
关于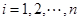 )的表达式;
)的表达式;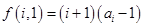 ,
,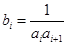 ,试求一个等比数列
,试求一个等比数列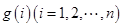 ,使得
,使得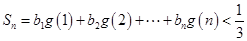 ,且对于任意的
,且对于任意的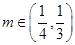 ,均存在实数
,均存在实数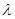 ?,当
?,当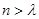 时,都有
时,都有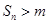 .
.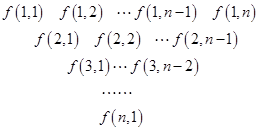
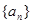 满足
满足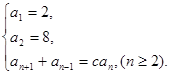 (
(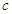 为常数,
为常数,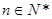 )
)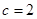 时,求
时,求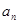 ;
;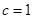 时,求
时,求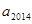 的值;
的值;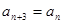 恒成立的常数
恒成立的常数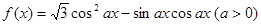 的图像与直线
的图像与直线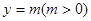 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为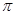 的等差数列.
的等差数列.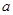 和
和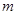 的值;
的值;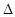 ABC中a、b、c分别是∠A、∠B、∠C的对边.若
ABC中a、b、c分别是∠A、∠B、∠C的对边.若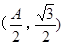 是函数
是函数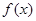 图象的一个对称中心,且a=4,求
图象的一个对称中心,且a=4,求