题目内容
已知| a |
| b |
| a |
| b |
分析：先利用数量积求出
•
，然后直接利用两角和与差的正弦函数公式得出所求式子等于sin135°，进而由特殊角的三角函数值得出答案．
| a |
| b |
解答：解：
•
=cos23°cos68°+cos67°cos22°
=sin67°cos68°+cos67°sin68°
=sin（67°+68°）
=sin135°
=
故答案为：
| a |
| b |
=sin67°cos68°+cos67°sin68°
=sin（67°+68°）
=sin135°
=
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查了两角和与差的余弦函数和向量的数量积，熟练掌握诱导公式以及特殊角的三角函数值是解题的关键，属于基础题．
练习册系列答案
相关题目
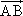＝(cos23°，cos67°)，
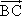＝(2cos68°，2cos22°)，则△ABC的面积为
=(cos23°,cos67°)，
=(cos68°,cos22°)，
=
+sinx，x∈[-a,a]的最大值
=(cos23°,cos67°)，
=(cos68°,cos22°)，
=
+sinx，x∈[-a,a]的最大值