题目内容
 21、如图,△ABC内接于圆⊙,点D是圆⊙上异于A、B、C三点的任意一点,过D点作DP⊥AB,DQ⊥BC,DR⊥AC,交AB、BC、AC分别为P,Q,R.
21、如图,△ABC内接于圆⊙,点D是圆⊙上异于A、B、C三点的任意一点,过D点作DP⊥AB,DQ⊥BC,DR⊥AC,交AB、BC、AC分别为P,Q,R.(1)求证:∠BDP=∠CDR;
(2)求证:P,Q,R三点共线.
分析:(1)由已知中四边形ABDC为圆内接四边形,根据圆内接四边形性质,我们易得∠DBP=∠DCP,结合已知中DP⊥AB,DR⊥AC,根据等角的余角相等,即可得到答案.
(2)由已知中DP⊥AB,DQ⊥BC,可判断出P、D、Q、B四点共圆,进而根据圆周角定理得到∠PQD=∠PBD,同理可得∠RQC=∠RDC,结合(1)中结论,我们易证明∠PQD+∠RQD=180°,进而得到P、Q、R三点共线.
(2)由已知中DP⊥AB,DQ⊥BC,可判断出P、D、Q、B四点共圆,进而根据圆周角定理得到∠PQD=∠PBD,同理可得∠RQC=∠RDC,结合(1)中结论,我们易证明∠PQD+∠RQD=180°,进而得到P、Q、R三点共线.
解答:证明:(1)由已知可得四边形ABDC为圆内接四边形
则∠DBP=∠DCP
又∵DP⊥AB,DR⊥AC,
∴∠BDP=90°-∠DBP,∠CDR=90°-∠DCP;
∴∠BDP=∠CDR;
(2)∵DP⊥AB,DQ⊥BC,
∴P、D、Q、B四点共圆
∴∠PQD=∠PBD
同理可得∠RQC=∠RDC
∵∠PBD+∠RDC=90°
∴∠PQD+∠RQD=90°+∠CQD=180°
故P、Q、R三点共线
则∠DBP=∠DCP
又∵DP⊥AB,DR⊥AC,
∴∠BDP=90°-∠DBP,∠CDR=90°-∠DCP;
∴∠BDP=∠CDR;
(2)∵DP⊥AB,DQ⊥BC,
∴P、D、Q、B四点共圆
∴∠PQD=∠PBD
同理可得∠RQC=∠RDC
∵∠PBD+∠RDC=90°
∴∠PQD+∠RQD=90°+∠CQD=180°
故P、Q、R三点共线
点评:本题考查的知识点是圆内接四边形的判定与性质,其中根据已知条件判断出P、D、Q、B四点共圆,进而根据圆周角定理得到∠PQD=∠PBD,并同理得到∠RQC=∠RDC,是证明三点共线的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=
如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=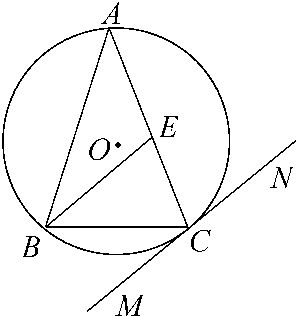 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.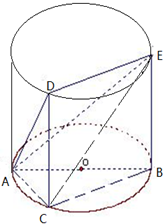 如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=
如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=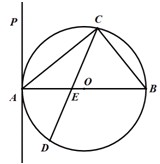 (2013•沈阳二模)选修4-1:几何证明选讲
(2013•沈阳二模)选修4-1:几何证明选讲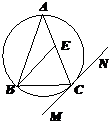 如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )
如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )