Question

已知函数f（x）=

3

sinωx•cosωx-cos²ωx+

3

2

（ω∈R，x∈R）的最小正周期为π，且图象关于直线x=

π

6

对称．
（1）求f（x）的解析式；
（2）若函数y=1-f（x）的图象与直线y=a在[0，

π

2

]上只有一个交点，求实数a的取值范围．

Answer 1

分析：（1）先根据两角和与差的公式和二倍角公式进行化简，再由最小正周期求出ω的值，最后根据图象关于直线x=

π

6

对称确定函数f（x）的解析式．
（2）将（1）中函数f（x）的解析式代入到y=1-f（x）中，然后在同一坐标系中画出y=1-f（x）与y=a的图象，进而根据图象可求出a的范围．

解答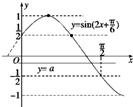：解：（1）∵f（x）=

3

sinωx•cosωx-cos²ωx+

3

2

=

3

2

sin2ωx-

1

2

（1+cos2ωx）+

3

2

=sin（2ωx-

π

6

）+1，
∵函数f（x）的最小正周期为π，
∴

2π

|2ω|

=π，即ω=±1，
∴f（x）=sin（±2x-

π

6

）+1．
①当ω=1时，f（x）=sin（2x-

π

6

）+1，
∴f（

π

6

）=sin

π

6

+1不是函数的最大值或最小值，
∴其图象不关于x=

π

6

对称，舍去．
②当ω=-1时，f（x）=-sin（2x+

π

6

）+1，
∴f（

π

6

）=-sin

π

2

+1=0是最小值，
∴其图象关于x=

π

6

对称．
故f（x）的解析式为f（x）=1-sin（2x+

π

6

）．
（2）∵y=1-f（x）=sin（2x+

π

6

）在同一坐标系中作出
y=sin（2x+

π

6

）和y=a的图象，
由图可知，直线y=a在a∈[-

1

2

，

1

2

)或a=1时，两曲线只有一个交点，
∴a∈[-

1

2

，

1

2

)或a=1．

点评：本题主要考查两角和与差的正弦公式和二倍角公式的应用和最小正周期的求法．考查三角函数基础知识的简单应用和灵活能力．