题目内容
若lgx,lg(x-2y),lgy三个数成等差数列,则
的值是( )
| x |
| y |
| A.1 | B.4 | C.1或
| D.1或4 |
∵lgx,lg(x-2y),lgy三个数成等差数列,
∴2lg(x-2y)=lgx+lgy,即(x-2y)2=xy,
整理得:x2-5xy+4y2=0,
等号两边同时除以y2得:(
)2-5•
+4=0,
解得:
=4或
=1,
又x>0,y>0,且x-2y>0,
∴
>2,
则
的值是4.
故选B
∴2lg(x-2y)=lgx+lgy,即(x-2y)2=xy,
整理得:x2-5xy+4y2=0,
等号两边同时除以y2得:(
| x |
| y |
| x |
| y |
解得:
| x |
| y |
| x |
| y |
又x>0,y>0,且x-2y>0,
∴
| x |
| y |
则
| x |
| y |
故选B

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 的值是( )
的值是( )
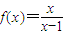 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;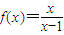 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;