题目内容
下列函数中,与函数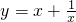 的奇偶性不同的是
的奇偶性不同的是
- A.

- B.

- C.

- D.
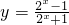
B
分析:根据题意,首先判断函数f(x)=x+ 的奇偶性,易得f(x)是奇函数;分别根据奇偶性的定义判断四个选项中函数的奇偶性,比较可得答案.
的奇偶性,易得f(x)是奇函数;分别根据奇偶性的定义判断四个选项中函数的奇偶性,比较可得答案.
解答:根据题意,对于f(x)=x+ ,易得f(-x)=-x-
,易得f(-x)=-x- ,即f(x)=-f(-x),则f(x)是奇函数;
,即f(x)=-f(-x),则f(x)是奇函数;
对于A,f(-x)=lg =lg
=lg -1=-lg
-1=-lg =-f(x),即f(x)=-f(-x),则f(x)是奇函数;
=-f(x),即f(x)=-f(-x),则f(x)是奇函数;
对于B,x>0时,f(-x)=-(-x)-1=x-1,x<0时,f(-x)=(-x)-1=-x-1,即f(x)=f(-x),则f(x)是偶函数;
对于C,x>0时,f(-x)=(-x)(1+x)=-[x(1+x)],x<0时,f(-x)=(-x)(1+x)=-[x(1-x)],又有f(0)=0;即f(x)=-f(-x),则f(x)是奇函数;
对于D,f(x)= ,f(-x)=
,f(-x)= =
= =
= =-
=- ,即f(x)=-f(-x),则f(x)是奇函数;
,即f(x)=-f(-x),则f(x)是奇函数;
可得,B中函数的奇偶性与函数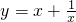 的奇偶性不同,
的奇偶性不同,
故选B.
点评:本题考查函数奇偶性的判断,对于分段函数的奇偶性的判断方法为分段求f(-x),对应区间找关系,综合全体下结论.
分析:根据题意,首先判断函数f(x)=x+
 的奇偶性,易得f(x)是奇函数;分别根据奇偶性的定义判断四个选项中函数的奇偶性,比较可得答案.
的奇偶性,易得f(x)是奇函数;分别根据奇偶性的定义判断四个选项中函数的奇偶性,比较可得答案.解答:根据题意,对于f(x)=x+
 ,易得f(-x)=-x-
,易得f(-x)=-x- ,即f(x)=-f(-x),则f(x)是奇函数;
,即f(x)=-f(-x),则f(x)是奇函数;对于A,f(-x)=lg
 =lg
=lg -1=-lg
-1=-lg =-f(x),即f(x)=-f(-x),则f(x)是奇函数;
=-f(x),即f(x)=-f(-x),则f(x)是奇函数;对于B,x>0时,f(-x)=-(-x)-1=x-1,x<0时,f(-x)=(-x)-1=-x-1,即f(x)=f(-x),则f(x)是偶函数;
对于C,x>0时,f(-x)=(-x)(1+x)=-[x(1+x)],x<0时,f(-x)=(-x)(1+x)=-[x(1-x)],又有f(0)=0;即f(x)=-f(-x),则f(x)是奇函数;
对于D,f(x)=
 ,f(-x)=
,f(-x)= =
= =
= =-
=- ,即f(x)=-f(-x),则f(x)是奇函数;
,即f(x)=-f(-x),则f(x)是奇函数;可得,B中函数的奇偶性与函数
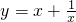 的奇偶性不同,
的奇偶性不同,故选B.
点评:本题考查函数奇偶性的判断,对于分段函数的奇偶性的判断方法为分段求f(-x),对应区间找关系,综合全体下结论.

练习册系列答案
相关题目