题目内容
某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是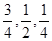 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为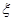 ,求
,求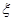 的分布列、数学期望和方差.
的分布列、数学期望和方差.
(1)
(2) 的分布列为:
的分布列为: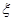
1 2 3 P 


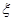 的数学期望
的数学期望

解析试题分析:(I)解:记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,“该选手通过决赛”为事件C,则 那么该选手在复赛阶段被淘汰的概率是
那么该选手在复赛阶段被淘汰的概率是 4分
4分
(II)解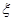 可能取值为1,2,3. 5分
可能取值为1,2,3. 5分
 的分布列为:
的分布列为: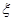
1 2 3 P 


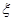 的数学期望
的数学期望 … 10
… 10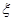 的方差
的方差 12分
12分
考点:分布列和期望值,方差
点评:主要是考查了独立事件概率的乘法公式以及分布列的求解,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 位,若连续抽取到两位愿意购买本地家禽的市民,或
位,若连续抽取到两位愿意购买本地家禽的市民,或 的分布列;
的分布列;  为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求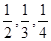 ,且每位同学能否通过考试时相互独立的。
,且每位同学能否通过考试时相互独立的。 ,求这三位同学中恰好有一位同学考上大学的概率。
,求这三位同学中恰好有一位同学考上大学的概率。 是从区间[0,3] 任 取 的一个数,
是从区间[0,3] 任 取 的一个数, 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.