题目内容
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点到其渐近线的距离等于双曲线的实轴长,则该双曲线的渐近线方程为y=±2x.分析 由已知中双曲线的焦点到其渐近线的距离等于实轴长,沟通a,b,c的关系,即可求出该双曲线的渐近线方程.
解答 解:∵焦点F(c,0)到渐近线y=$\frac{b}{a}$x的距离等于实轴长,
∴$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=2a,
∴b=2a,
即有双曲线的渐近线方程为y=±$\frac{b}{a}$x,
即为y=±2x.
故答案为:y=±2x.
点评 本题考查的知识点是双曲线的简单性质,双曲线的渐近线的求法,通过a,b,c的比例关系,可以求渐近线方程,也可以求离心率.

练习册系列答案
相关题目
5.记集合T={0,1,2,3,4,5,6,7,8,9},$M=\{\frac{a_1}{10}+\frac{a_2}{{{{10}^2}}}+\frac{a_3}{{{{10}^3}}}+\frac{a_4}{{{{10}^4}}}|{a_i}∈T,i=1,2,3,4\}$,将M中的元素按从大到小排列,则第2012个数是( )
| A. | $\frac{5}{10}+\frac{5}{{{{10}^2}}}+\frac{7}{{{{10}^3}}}+\frac{3}{{{{10}^4}}}$ | B. | $\frac{5}{10}+\frac{5}{{{{10}^2}}}+\frac{7}{{{{10}^3}}}+\frac{2}{{{{10}^4}}}$ | ||
| C. | $\frac{7}{10}+\frac{9}{{{{10}^2}}}+\frac{8}{{{{10}^3}}}+\frac{8}{{{{10}^4}}}$ | D. | $\frac{7}{10}+\frac{9}{{{{10}^2}}}+\frac{9}{{{{10}^3}}}+\frac{1}{{{{10}^4}}}$ |
9.阅读程序框图,如果输出i=5,那么在空白矩形框中填入的语句为( )


| A. | S=2*i+4 | B. | S=2*i-1 | C. | S=2*i-2 | D. | S=2*i |
6.双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的右焦点坐标为( )
| A. | (5,0) | B. | (0,5) | C. | ($\sqrt{7}$,0) | D. | (0,$\sqrt{7}$) |
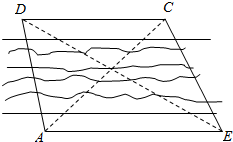 为了测量河对岸两个建筑物C、D之间的距离,在河岸边取点A、B,∠BAC=45°,∠DAC=75°,∠ABD=30°,∠DBC=45°,AB=$\sqrt{3}$千米,A、B、C、D在同一个平面内,试求C、D之间的距离.
为了测量河对岸两个建筑物C、D之间的距离,在河岸边取点A、B,∠BAC=45°,∠DAC=75°,∠ABD=30°,∠DBC=45°,AB=$\sqrt{3}$千米,A、B、C、D在同一个平面内,试求C、D之间的距离.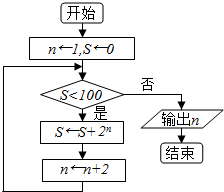
 如图,△ABC是直角三角形,∠C为直角,D是斜边AB上一点,以BD为直径的圆O与AC相切于点E,与BC相交于点F.
如图,△ABC是直角三角形,∠C为直角,D是斜边AB上一点,以BD为直径的圆O与AC相切于点E,与BC相交于点F.