题目内容
(12分)定义运算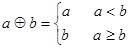 若函数
若函数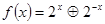 .
.
(1)求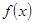 的解析式;
的解析式;
(2)画出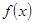 的图像,并指出单调区间、值域以及奇偶性.
的图像,并指出单调区间、值域以及奇偶性.
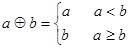 若函数
若函数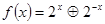 .
.(1)求
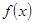 的解析式;
的解析式;(2)画出
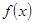 的图像,并指出单调区间、值域以及奇偶性.
的图像,并指出单调区间、值域以及奇偶性.(1) ;(2)
;(2)  在
在 上单调递增, 在
上单调递增, 在 上单调递减;值域为
上单调递减;值域为
 ;(2)
;(2)  在
在 上单调递增, 在
上单调递增, 在 上单调递减;值域为
上单调递减;值域为
试题分析:(1)根据
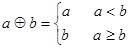 表示取a与b中较小的可知只需比较
表示取a与b中较小的可知只需比较 与
与 的大小关系即可得到结论.(2)由分段函数与指数函数性质画出图像,由图像可得出单调区间、值域以及奇偶性.
的大小关系即可得到结论.(2)由分段函数与指数函数性质画出图像,由图像可得出单调区间、值域以及奇偶性.试题解析:
(1)由
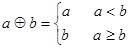 ,知
,知
(2)
 的图像如图:
的图像如图:
 在
在 上单调递增, 在
上单调递增, 在 上单调递减
上单调递减值域为


练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 元.公司拟投入
元.公司拟投入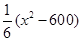 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价. ,如果每年平均增长5﹪,经过
,如果每年平均增长5﹪,经过 年,树林中有木材
年,树林中有木材
 ,
, )
) ,
, ,给出下列四个图形,其中能表示以
,给出下列四个图形,其中能表示以 为定义域,
为定义域, 为值域的函数关系的是( ).
为值域的函数关系的是( ).
 ,
, ,
, ,下列函数中不满足其中任何一个等式的是( )
,下列函数中不满足其中任何一个等式的是( )



 ,若存在区间
,若存在区间 ,当
,当 时,函数
时,函数 ,则称
,则称 倍值函数. 若
倍值函数. 若 是
是 关于时间
关于时间 的函数关系式分别为
的函数关系式分别为 ,
, ,
, ,
, ,有以下结论:
,有以下结论: 时,甲走在最前面;
时,甲走在最前面; 时,丁走在最前面,当
时,丁走在最前面,当 表示不大于
表示不大于 的最大整数,则函数
的最大整数,则函数 的零点之积为( )
的零点之积为( )

 ,则
,则 的表达式为 .
的表达式为 .