题目内容
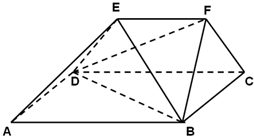 如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC.
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC.(1)求证:平面ABFE⊥平面DCFE;
(2)求四面体B-DEF的体积.
分析:(1)因为∠BFC=90°,所以FC⊥BF,又因为EF⊥FB,根据线面垂直的判定定理可得:BF⊥平面EFCD,进而得到面面垂直.
(2)根据四边形ABCD为正方形,可得AB⊥BC.进而可得EF⊥BC,而EF⊥BF,结合线面垂直的判定定理可得EF⊥面BCF,
所以EF⊥FC,即FC是△DEF的边EF上的高,由(1)得:BF的长为B到面DEF的距离,进而求出答案.
(2)根据四边形ABCD为正方形,可得AB⊥BC.进而可得EF⊥BC,而EF⊥BF,结合线面垂直的判定定理可得EF⊥面BCF,
所以EF⊥FC,即FC是△DEF的边EF上的高,由(1)得:BF的长为B到面DEF的距离,进而求出答案.
解答: 解:(1)因为∠BFC=90°,
解:(1)因为∠BFC=90°,
所以FC⊥BF,
又因为EF⊥FB,又FC∩EF=F,并且FC,EF?平面EFCD,
所以BF⊥平面EFCD,
因为BF?平面ABEF,
所以平面ABFE⊥平面DCFE.
(2)∵四边形ABCD为正方形,则AB⊥BC
又EF∥AB,则EF⊥BC,而EF⊥BF,BF∩BC=B且BF,BC?面BCF
所以:EF⊥面BCF,而FC?面BCF,则:EF⊥FC
即FC是△DEF的边EF上的高,
由(1)得:BF⊥面EFCD,即:BF的长为B到面DEF的距离,
所以:VB-DEF=
S△DEF•BF=
•(
•1•
)•
=
.
 解:(1)因为∠BFC=90°,
解:(1)因为∠BFC=90°,所以FC⊥BF,
又因为EF⊥FB,又FC∩EF=F,并且FC,EF?平面EFCD,
所以BF⊥平面EFCD,
因为BF?平面ABEF,
所以平面ABFE⊥平面DCFE.
(2)∵四边形ABCD为正方形,则AB⊥BC
又EF∥AB,则EF⊥BC,而EF⊥BF,BF∩BC=B且BF,BC?面BCF
所以:EF⊥面BCF,而FC?面BCF,则:EF⊥FC
即FC是△DEF的边EF上的高,
由(1)得:BF⊥面EFCD,即:BF的长为B到面DEF的距离,
所以:VB-DEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
点评:解决此类问题的关键是熟练掌握几何体的结构特征,利用线线的垂直关系证明线面垂直与面面垂直,进而求出几何体积.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC, (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC, (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=