题目内容
已知a>b>c,且a+b+c=0,求证: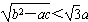 。
。
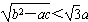 。
。解:要证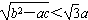 ,只需证b2-ac<3a2
,只需证b2-ac<3a2
∵a+b+c=0,
只需证b2+a(a+b)<3a2,
只需证2a2-ab-b2>0,
只需证(a-b)(2a+b)>0,
只需证(a-b)(a-c)>0
因为a>b>c,
所以a-b>0,a-c>0,
所以(a-b)(a-c)>0,显然成立
故原不等式成立。
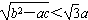 ,只需证b2-ac<3a2
,只需证b2-ac<3a2∵a+b+c=0,
只需证b2+a(a+b)<3a2,
只需证2a2-ab-b2>0,
只需证(a-b)(2a+b)>0,
只需证(a-b)(a-c)>0
因为a>b>c,
所以a-b>0,a-c>0,
所以(a-b)(a-c)>0,显然成立
故原不等式成立。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目