Question

（本小题满分12分）
将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，AE⊥平面ABD，且AE＝．

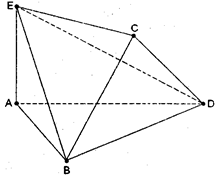
（Ⅰ）求证：DE⊥AC；
（Ⅱ）求DE与平面BEC所成角的正弦值；
（Ⅲ）直线BE上是否存在一点M，使得CM∥平面ADE，若存在，求点M的位置，不存在请说明理由．

Answer 1

解：（Ⅰ）以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系

则,,
做BD的中点F并连接CF，AF；由题意可得CF⊥BD且
又 ，所以C的坐标为
，
  
故DE⊥AC                                                    　　　 ………4分
（Ⅱ）设平面BCE的法向量为则
  即
令x=1得   又                       　　 ………6分
设平面DE与平面BCE所成角为，则
.                           　………8分
(III)假设存在点M使得CM∥面ADE，则
, 得    　………10分
又因为， 所以
因为CM∥面ADE，则即
得
故 点M为BE的中点时CM∥面ADE.                                  　 ………12分

解析