题目内容
已知函数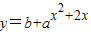 (a、b是常数且a>0,a≠1)在区间[-
(a、b是常数且a>0,a≠1)在区间[- ,0]上有ymax=3,ymin=
,0]上有ymax=3,ymin= ,试求a和b的值.
,试求a和b的值.
【答案】分析:先将x2+2x看作整体,由u=x2+2x的单调性得到最值,再利用复合函数的单调性求得函数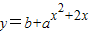 的最值.
的最值.
解答:解:解:令u=x2+2x=(x+1)2-1x∈[- ,0](1分)
,0](1分)
∴当x=-1时,umin=-1当x=0时,umax=0(3分)
1)当a>1时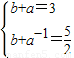 解得
解得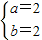
2)当0<a<1时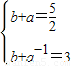 解得
解得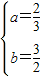
综上得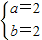 或
或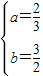
点评:本题通过最值来考查复合函数的单调性的研究.
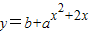 的最值.
的最值.解答:解:解:令u=x2+2x=(x+1)2-1x∈[-
 ,0](1分)
,0](1分)∴当x=-1时,umin=-1当x=0时,umax=0(3分)
1)当a>1时
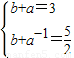 解得
解得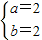
2)当0<a<1时
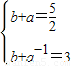 解得
解得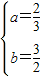
综上得
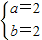 或
或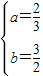
点评:本题通过最值来考查复合函数的单调性的研究.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=3•2x-1,则当x∈N时,数列{f(n+1)-f(n)}( )
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |
 (a∈R),下列说法正确的是( )
(a∈R),下列说法正确的是( ) ,则
,则 ;
;