题目内容
 如图,B,C分别是∠A两边上的动点,在△ABC中,A,B,C的对边分别是a,b,c,已知3acosA=ccosB+bcosC.
如图,B,C分别是∠A两边上的动点,在△ABC中,A,B,C的对边分别是a,b,c,已知3acosA=ccosB+bcosC.(Ⅰ)求cosA的值;
(Ⅱ)若a=2,试求△ABC面积的最大值.
分析:(I)通过正弦定理以及两角和的正弦函数化简表达式,求出A的大小.
(II)通过余弦定理以及基本不等式求出bc的最大值,然后求出面积的最大值.
(II)通过余弦定理以及基本不等式求出bc的最大值,然后求出面积的最大值.
解答:解:(I)因为3acosA=ccosB+bcosC,
由正弦定理可知3sinAcosA=sinCcosB+sinBcosC,
即sin(B+C)=3sinAcosA,
在三角形中,B+C=π-A,∴sinA=3sinAcosA
∴cosA=
.
(II)∵a2=b2+c2-2bccosA,
∴
bc=b2+c2-4≥2bc-4
∴bc≤3,
∵cosA=
∴sinA=
∴S△ABC=
bcsinA≤
×3×
=
当且仅b=c=
时取等号
∴△ABC面积的最大值是
.
由正弦定理可知3sinAcosA=sinCcosB+sinBcosC,
即sin(B+C)=3sinAcosA,
在三角形中,B+C=π-A,∴sinA=3sinAcosA
∴cosA=
| 1 |
| 3 |
(II)∵a2=b2+c2-2bccosA,
∴
| 2 |
| 3 |
∴bc≤3,
∵cosA=
| 1 |
| 3 |
∴sinA=
2
| ||
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
| 2 |
当且仅b=c=
| 3 |
∴△ABC面积的最大值是
| 2 |
点评:本题考查正弦定理与余弦定理的应用,考查三角形的面积的求法,考查计算能力.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 5、阅读如图所示的程序框图,若输入的a,b,c分别为21,32,75,则输出的a,b,c分别是( )
5、阅读如图所示的程序框图,若输入的a,b,c分别为21,32,75,则输出的a,b,c分别是( )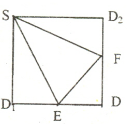 如图,E、F分别是正方形SD1DD2的边D1D、DD2的中点,沿SE、SF、EF将它折成一个几何体,使D1、D、D2重合,记作D,给出下列位置关系:①SD⊥面EFD; ②SE⊥面EFD;③DF⊥SE;④EF⊥面SED.其中成立的有( )
如图,E、F分别是正方形SD1DD2的边D1D、DD2的中点,沿SE、SF、EF将它折成一个几何体,使D1、D、D2重合,记作D,给出下列位置关系:①SD⊥面EFD; ②SE⊥面EFD;③DF⊥SE;④EF⊥面SED.其中成立的有( )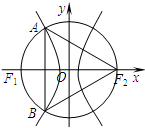 如图,F1和F2分别是双曲线
如图,F1和F2分别是双曲线