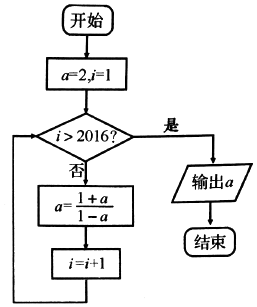
题目内容
【题目】已知矩形ABCD（AB＞AD）的周长为12，若将它关于对角线AC折起后，使边AB与CD交于点P（如图所示），则△ADP面积的最大值为 ．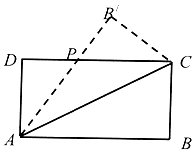 
【答案】27﹣18 
【解析】解∵设AB=x，则AD=6﹣x，又DP=PB′，AP=AB′﹣PB′=AB﹣DP，
即AP=x﹣DP，
∴（6﹣x）2+PD2=（x﹣PD）2，得PD=6﹣ 
，
∵AB＞AD，
∴3＜x＜6，
∴△ADP的面积S= 
ADDP= （6﹣x）（6﹣ ）
=27﹣3（x+ ）≤27﹣3×2 
=27﹣18 
，
当且仅当x=3 时取等号，
∴△ADP面积的最大值为27﹣18 ，
所以答案是：27﹣18
【考点精析】认真审题，首先需要了解基本不等式(基本不等式：
,（当且仅当
时取到等号）；变形公式：
)．
练习册系列答案
灵星计算小达人系列答案
相关题目
