题目内容
已知抛物线 ,过其对称轴上一点
,过其对称轴上一点 作一直线交抛物线于A,B两点,若∠OBA=60°,求OB的斜率.
作一直线交抛物线于A,B两点,若∠OBA=60°,求OB的斜率.
【答案】分析:先设直线AB的方程和A,B两点的坐标,然后联立直线AB和抛物线消去x得到y的二次方程,进而可表示出两根之和,再结合直线AB方程可得到其横坐标之积的值,进而可得到OA⊥OB,最后根据∠OBA=60°可求出B点的纵坐标的值,然后根据横纵坐标之间的关系得到OB的斜率.
解答:解:设直线AB方程为 ,
,
A(x1,y1),B(x2,y2),
则由 ,得
,得 ,
,
则y1•y2=-12,x1•x2=12,
∴x1•x2+y1•y2=0,∴OA⊥OB,又∠OBA=60°,
∴ ,∴x12+y12=3(x22+y22),
,∴x12+y12=3(x22+y22),
∴ ,∴
,∴ ,
,
∴ .
.
点评:本题主要考查直线和抛物线的综合问题.直线和圆锥曲线的综合题是高考的热点,也是难点,要强化复习.
解答:解:设直线AB方程为
 ,
,A(x1,y1),B(x2,y2),
则由
 ,得
,得 ,
,则y1•y2=-12,x1•x2=12,
∴x1•x2+y1•y2=0,∴OA⊥OB,又∠OBA=60°,
∴
 ,∴x12+y12=3(x22+y22),
,∴x12+y12=3(x22+y22),∴
 ,∴
,∴ ,
,∴
 .
.点评:本题主要考查直线和抛物线的综合问题.直线和圆锥曲线的综合题是高考的热点,也是难点,要强化复习.

练习册系列答案
相关题目
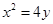 ,过定点
,过定点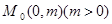 的直线
的直线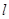 交抛物线于A、B两点.
交抛物线于A、B两点.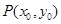 在定直线
在定直线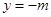 上.
上. 时,在抛物线上存在不同的两点P、Q关于直线
时,在抛物线上存在不同的两点P、Q关于直线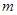 表示),若不存在,请说明理由.
表示),若不存在,请说明理由.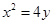 ,过定点
,过定点 的直线
的直线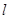 交抛物线于A、B两点.
交抛物线于A、B两点. 在定直线
在定直线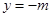 上.
上.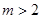 时,在抛物线上存在不同的两点P、Q关于直线
时,在抛物线上存在不同的两点P、Q关于直线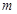 表示),若不存在,请说明理由.
表示),若不存在,请说明理由.