Question

如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60⁰，Q为AD中点.

（1）若PA=PD，求证：平面PQB⊥平面PAD；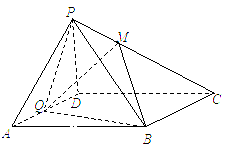

（2）点M在线段PC上，PM=tPC，试确定实数t的值，使得PA//平面MQB.

Answer 1

同下

解析:

（1）因为PA＝PD，Q为AD的中点，所以PQ^AD．

连接BD，因为ABCD为菱形，??DAB＝60°，所以AB＝BD．所以BQ^AD．………2分

因为BQ??平面PQB，PQ??平面PQB，BQ∩PQ＝Q．所以AD^平面PQB．…………2分

因为AD??平面PAD，所以平面PQB^平面PAD．………………………………………2分

（2）当且仅当t＝时，PA∥平面MQB．…………………………………………2分

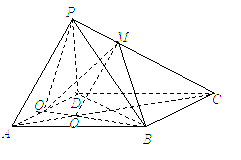
证明如下：

连接AC，设AC∩BQ＝O，连接OM．

在△AOQ与△COB中，

因为AD∥BC，

所以??OQA＝??OBC，??OAQ＝??OCB．

所以△AOQ∽△COB．

所以＝＝．所以＝． ……2分

在△CAP与△COM中，当t＝时，因为＝＝，??ACP＝??OCM，

所以△CAP∽△COM．所以??CPA＝??CMO．所以AP∥OM． ……………………2分

因为OM??平面MQB，PA(/平面MQB，

所以PA∥平面MQB．以上每步可逆，当PA∥平面MQB可得t＝  ……………2分