题目内容
已知函数
．
（1）若
在
上存在零点，求实数
的取值范围；
（2）当
时，若对任意的
，总存在
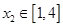使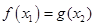
成立，求实数
的取值范围．
（1）
；（2）
．
解析试题分析：（1）在
上存在零点，只需
即可；
（2）本问是存在性问题，只需函数的值域为函数
的值域的子集即可．
试题解析：（1）
的对称轴为
，所以在上单调递减，且函数在存在零点，所以
即
解得
．
故实数的取值范围为．
（2）由题可知函数的值域为函数
的值域的子集
，
以下求函数
的值域：
①
时，
为常函数，不符合题意；
②
，
，∴
解得
；
③
，
，∴
解得
．
综上所述，的取值范围为．
考点：1.函数的零点；2.恒成立问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价P(元/件)：前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如表：
| 时间(将第x天记为x)x | 1 | 10 | 11 | 18 |
| 单价(元/件)P | 9 | 0 | 1 | 8 |
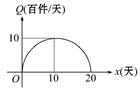
(1)写出每天销售收入y(元)与时间x(天)的函数关系式y=f(x).
(2)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价P定为多少元为好?(结果精确到1元)
（单位：千米/小时）是车流密度
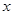（单位：辆/千米）的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当
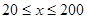时，车流速度
时，求函数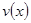
的表达式；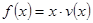
可以达到最大，并求出最大值．（精确到1辆/小时）
（万元）与处理量
（吨）之间的函数关系可近似的表示为：
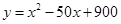，且每处理一吨废弃物可得价值为
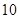万元的某种产品，同时获得国家补贴
时，判断该项举措能否获利？如果能获利，求出最大利润；
在区间[－1，1]上是增函数．
的两个相异实根，若对任意a∈A及t∈[－1，1]，不等式m2＋tm＋1≥|x1－x2|恒成立，求实数m的取值范围．
×
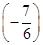0＋80.25×
＋(
×
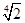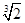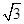)6－
；
；
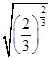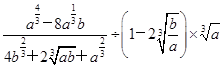
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+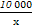
-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.